Phương pháp giải:

+) Lập bảng giá trị sau đó vẽ đồ thị hàm số.

+) Đường thẳng \(y = {a_1}x + {b_1}\) và \(y = {a_2}x + {b_2}\) song song với nhau \( \Leftrightarrow \left\{ \begin{array}{l}{a_1} = {a_2}\\{b_1} \ne {b_2}\end{array} \right..\) 

Lời giải chi tiết:

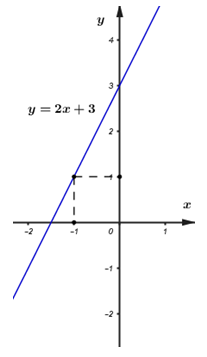
a) Vẽ đồ thị hàm số \(y = 2x + 3.\)

Ta có bảng giá trị:

Vậy đồ thị hàm số \(y = 2x + 3\) là đường thẳng đi qua các điểm \(\left( {0;\;3} \right),\;\;\left( { - 1;\;1} \right).\)

b) Xác định \(m\) để đồ thị của hàm số \(y = 2x + 3\) song song với đồ thị hàm số \(y = \left( {{m^2} - 2m + 2} \right)x + 2m - 1.\)

Đường thẳng  \(y = 2x + 3\) song song với đường thẳng \(y = \left( {{m^2} - 2m + 2} \right)x + 2m - 1 \Leftrightarrow \left\{ \begin{array}{l}{m^2} - 2m + 2 = 2\\2m - 1 \ne 3\end{array} \right.\)

\( \Leftrightarrow \left\{ \begin{array}{l}{m^2} - 2m = 0\\2m \ne 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}m = 0\\m = 2\end{array} \right.\\m \ne 2\end{array} \right. \Leftrightarrow m = 0.\)

Vậy \(m = 0\) thỏa mãn yêu cầu bài toán.

Chọn C.