Câu hỏi
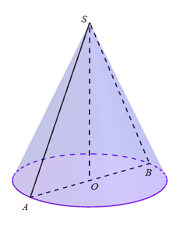
Một hình nón có chiều cao bằng a và thiết diện qua trục của hình nón đó là tam giác vuông. Tính theo a diện tích xung quanh của hình nón đó.
- A \(\frac{{\sqrt 2 \pi }}{2}{a^2}\).
- B \(2\pi {a^2}\).
- C \(2\sqrt 2 \pi {a^2}\).
- D \(\sqrt 2 \pi {a^2}\).
Phương pháp giải:
Diện tích xung quanh của khối nón: \({S_{xq}} = \pi Rl\)
Lời giải chi tiết:
Theo đề bài, ta có tam giác SAB là tam giác vuông cân tại S, SO = a
\( \Rightarrow \)\(R = OA = SO = a\)
Độ dài đường sinh: \(l = SA = OA.\sqrt 2 = a\sqrt 2 \)
Diện tích xung quanh của khối nón: \({S_{xq}} = \pi Rl = \pi .a.a\sqrt 2 = \sqrt 2 \pi {a^2}\).
Chọn: D
Câu hỏi trước
