Câu hỏi
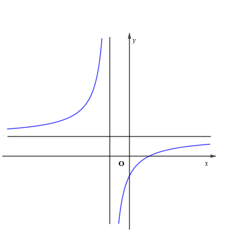
Cho hàm số \(y = \frac{{ax + b}}{{x - c}}\) có đồ thị như hình vẽ bên. Tìm khẳng định đúng trong các khẳng định sau
- A \(a > 0,\,b < 0,\,c > 0\).
- B \(a > 0,\,b > 0,\,c < 0\).
- C \(a > 0,\,b < 0,\,c < 0\).
- D \(a < 0,\,b > 0,\,c > 0\).
Phương pháp giải:
Đồ thị hàm số \(y = \frac{{ax + b}}{{x - c}}\) có hai đường tiệm cận: \(x = c\) và \(y = a\), đồng thời cắt trục hoành tại điểm \(\left( { - \frac{b}{a};0} \right)\)
Lời giải chi tiết:
Quan sát đồ thị hàm số ta thấy: Đồ thị hàm số có tiệm cận đứng \(x = {x_0} < 0 \Rightarrow c < 0\), đồ thị hàm số có tiệm cận ngang \(y = {y_0} > 0 \Rightarrow a > 0\)
Đồ thị hàm số cắt trục hoành tại điểm
\(\left( x_{0}^{'};0 \right),x_{0}^{'}>0\Rightarrow -\frac{b}{a}>0\)
Mà \(a > 0 \Rightarrow b < 0\)
Vậy, \(a > 0,\,b < 0,\,c < 0\).
Chọn: C