Phương pháp giải:

Mặt cầu tâm A tiếp xúc với (SBC) có bán kính \(R = d\left( {A;\left( {SBC} \right)} \right)\)

Diện tích mặt cầu: \({S_{mc}} = 4\pi {R^2}\).

Lời giải chi tiết:

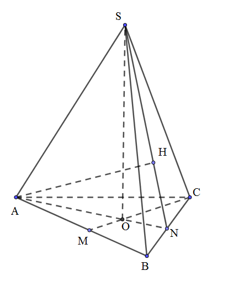
Gọi M, N lần lượt là trung điểm của AB, BC; O là giao điểm của AN và CM. Kẻ \(AH \bot SN\,\,\left( {H \in SN} \right)\).

Tam giác ABC đều, tâm O \( \Rightarrow OA = \frac{2}{3}AN = \frac{2}{3}.\frac{{3\sqrt 3 }}{2} = \sqrt 3 \)

Tam giác SAO vuông tại O \( \Rightarrow SO = \sqrt {S{A^2} - O{A^2}}  = \sqrt {6 - 3}  = \sqrt 3 \)

Tam giác SBC cân tại N \( \Rightarrow SN \bot BC \Rightarrow \)Tam giác SNC vuông tại N

\( \Rightarrow SN = \sqrt {S{B^2} - B{N^2}}  = \sqrt {6 - {{\left( {\frac{3}{2}} \right)}^2}}  = \frac{{\sqrt {15} }}{2}\)

Tam giác AHN đồng dạng tam giác SON \( \Rightarrow \frac{{AH}}{{SO}} = \frac{{AN}}{{SN}} \Leftrightarrow \frac{{AH}}{{\sqrt 3 }} = \frac{{\frac{{3\sqrt 3 }}{2}}}{{\frac{{\sqrt {15} }}{2}}} = \frac{3}{{\sqrt 5 }}\) \( \Rightarrow AH = \frac{{3\sqrt 3 }}{{\sqrt 5 }}\)

Diện tích mặt cầu: \({S_{mc}} = 4\pi {R^2} = 4\pi .{\left( {\frac{{3\sqrt 3 }}{{\sqrt 5 }}} \right)^2} = \frac{{108\pi }}{5}\).

Chọn: B