Câu hỏi
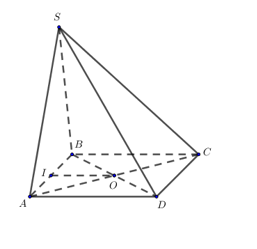
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Mặt bên SAB là tam giác vuông tại S và nằm trong mặt phẳng vuông góc với đáy. Tính diện tích S của mặt cầu ngoại tiếp khối chóp S.ABCD?
- A \(S = 2\pi {a^2}\)
- B \(S = 8\pi {a^2}\)
- C \(S = \pi {a^2}\)
- D \(S = 4\pi {a^2}\)
Phương pháp giải:
+) Xác định tâm đường tròn ngoại tiếp tứ giác ABCD và tam giác SAB.
+) Dựng hai trục của hai mặt SAB và ABCD.
+) Xác định giao điểm của hai trục vừa dựng, đó chính là tâm mặt cầu ngoại tiếp chóp.
Lời giải chi tiết:
Gọi I là trung điểm của AB ta có \(OI \bot AB \Rightarrow OI \bot \left( {SAB} \right)\)
Tam giác SAB vuông tại S nên I là tâm đường tròn ngoại tiếp tam giác SAB.
\( \Rightarrow OS = OA = OB\)
Lại có \(OA = OB = OC = OD\)
\( \Rightarrow OS = OA = OB = OC = OD \Rightarrow O\) là tâm mặt cầu ngoại tiếp khối chóp S.ABCD
Khi đó bán kính mặt cầu ngoại tiếp khối chóp là \(R = OA = \frac{{a\sqrt 2 }}{2} \Rightarrow S = 4\pi {R^2} = 4\pi .\frac{{{a^2}}}{2} = 2\pi {a^2}\)
Chọn A.