Câu hỏi
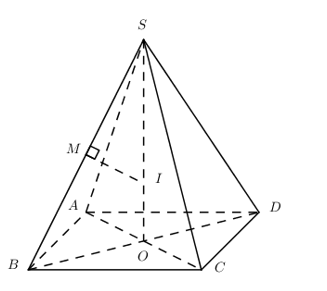
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng 2a. Tính thể tích V của khối cầu ngoại tiếp khối chóp S.ABCD.
- A \(V = \frac{{64\pi {a^3}}}{3}\)
- B \(V = 8\pi {a^2}\)
- C \(V = \frac{{32\pi {a^3}}}{3}\)
- D \(V = \frac{{8\sqrt 2 \pi {a^3}}}{3}\)
Phương pháp giải:
Thể tích khối cầu bán kính R là \(V = \frac{4}{3}\pi {R^3}\)
Lời giải chi tiết:
Gọi O là tâm hình vuông ABCD \( \Rightarrow SO \bot \left( {ABCD} \right)\).
Gọi M là trung điểm của SB.
Trong (SBD) qua M kẻ \(MI \bot SB\,\,\left( {I \in SO} \right) \Rightarrow I\)là tâm khối cầu ngoại tiếp chóp S.ABCD.
Xét tam giác vuông SAO có:
\(SO = \sqrt {S{A^2} - O{A^2}} = \sqrt {4{a^2} - {{\left( {a\sqrt 2 } \right)}^2}} = a\sqrt 2 \)
Ta có \(\Delta SOB \sim \Delta SMI \Rightarrow \frac{{SI}}{{SB}} = \frac{{SM}}{{SO}} \Rightarrow SI = \frac{{2a.a}}{{a\sqrt 2 }} = a\sqrt 2 \)
\( \Rightarrow {V_{cau}} = \frac{4}{3}\pi {\left( {a\sqrt 2 } \right)^3} = \frac{{8\sqrt 2 \pi {a^3}}}{3}\)
Chọn D.