Câu hỏi
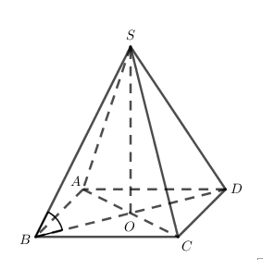
Cho hình chóp đều S.ABCD có cạnh đáy bằng 2a, góc giữa cạnh bên và mặt đáy bằng 600. Thể tích V của hình chóp S.ABCD.
- A \(V = \frac{{4{a^3}\sqrt 3 }}{3}\)
- B \(V = 4\sqrt 3 {a^3}\)
- C \(V = \frac{{4{a^3}\sqrt 6 }}{3}\)
- D \(V = 4{a^2}\sqrt 6 \)
Phương pháp giải:
Gọi O là tâm hình vuông ABCD \( \Rightarrow {V_{S.ABCD}} = \frac{1}{3}SO.{S_{ABCD}}\)
Lời giải chi tiết:
Gọi O là tâm hình vuông ABCD
\( \Rightarrow SO \bot (ABCD) \Rightarrow = \angle (SB,OB) = \angle SBO = {60^0}\)
\(\begin{array}{l} \Rightarrow SO = OB.\tan {60^0} = \frac{{2a\sqrt 2 }}{2}.\sqrt 3 = a\sqrt 6 \\ \Rightarrow {V_{S.ABCD}} = \frac{1}{3}SO.{S_{ABCD}} = \frac{1}{3}a\sqrt 6 .4{a^2} = \frac{{4{a^3}\sqrt 6 }}{3}\end{array}\)
Chọn C.
Câu hỏi trước
