Câu hỏi
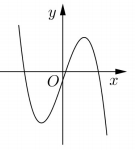
Cho hàm số \(y = a{x^3} + b{x^2} + cx + d\,\,\left( {a,b,c,d \in R} \right)\) có đồ thị như hình vẽ bên. Số điểm cực trị của hàm số đã cho là:
- A 0
- B 1
- C 3
- D 2
Phương pháp giải:
Cho hàm số \(y = f\left( x \right)\) có đạo hàm trong lân cận V của \({x_0}\). Nếu \(f\left( x \right)\) đối dấu khi \(x\) đi qua \({x_0}\) thì \(f\left( x \right)\) đạt cực trị tại \({x_0}\).
Lời giải chi tiết:
Dựa vào đồ thị trên ta thấy hàm số đã cho có 2 cực trị.
Chọn D.
Câu hỏi trước
