Câu hỏi
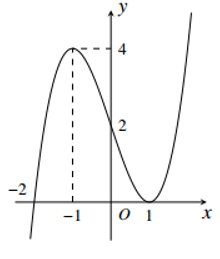
Cho hàm số \(y=f\left( x \right)\) có đạo hàm liên tục trên R. Đồ thị hàm số \(y=f'\left( x \right)\) như hình vẽ .
Số điểm cực trị của hàm số \(g\left( x \right)=f\left( x \right)-4x\) là :
- A 2
- B 3
- C 1
- D 4
Phương pháp giải:
Nếu đạo hàm của hàm số đổi dấu khi đi qua x=a thì a là một cực trị của hàm số
Lời giải chi tiết:
\(g'\left( x \right)=f'\left( x \right)-4\)
Ta tịnh tiến đồ thị hàm số \(y=f'\left( x \right)\) xuống 4 đơn vị dọc theo trục Oy sẽ được đồ thị hàm số \(g'\left( x \right)=f'\left( x \right)-4\) . Nhận thấy đồ thị hàm số \(g'\left( x \right)=f'\left( x \right)-4\) chỉ cắt Ox tại hai điểm nhưng tại điểm x= -1 thì không đổi dấu => hàm số \(g\left( x \right)\) chỉ có 1 cực trị
Chọn đáp án C