Phương pháp giải:

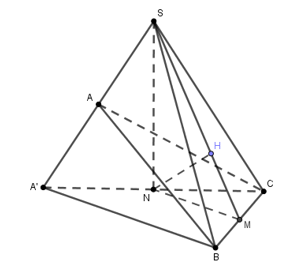
Tính khoảng cách từ A đến mặt phẳng (SBC) thông qua khoảng cách từ A’ đến mặt phẳng (SBC), thông qua khoảng cách từ A’ đến mặt phẳng (SBC) (với A’ là điểm đối xứng của S qua A và N là trung điểm A’C)

Lời giải chi tiết:

Theo đề bài, ta có: các tam giác \(SAB,\,\,SBC\) có:  \(\widehat{ASB}=\widehat{CSB}={{60}^{0}}\) và \(SA'=\,\,SB=SC=2a\)

\(\Rightarrow \Delta SAB,\,\,\Delta SBC\) đều, cạnh bằng 2a.

\(\Delta SA'C\) vuông cân tại S \(\Rightarrow A'C=SA'.\sqrt{2}=2\sqrt{2}a\)

\(\Rightarrow \Delta A'BC\) vuông cân tại B

Gọi N là trung điểm của A’C \(\Rightarrow SN\bot (A'BC)\)

Gọi M là trung điểm của BC \(\Rightarrow MN//A'B\). Mà \(A'B\bot BC\Rightarrow MN\bot BC\Rightarrow BC\bot (SMN)\)

Ta có: \(A'S\cap (SBC)=S,\,\,A'S=2AS\Rightarrow d\left( A;\left( SBC \right) \right)=\frac{1}{2}d\left( A';\left( SBC \right) \right)\)

Mặt khác: \(A'C\cap (SBC)=C,\,\,A'C=2NC\Rightarrow d\left( A';\left( SBC \right) \right)=2d\left( N;\left( SBC \right) \right)\)

\(\Rightarrow d\left( A;\left( SBC \right) \right)=d\left( N;\left( SBC \right) \right)\)

Trong \(\left( SMN \right)\), kẻ \(NH\bot SM\Rightarrow SM\bot (SBC)\Rightarrow d\left( N;(SBC) \right)=NH\Rightarrow d\left( A;\left( SBC \right) \right)=NH\)

+) Tính NH:

Ta có: \(MN=\frac{1}{2}A'B=\frac{1}{2}.2a=a\)(vì \(\Delta SA'B\) đều, cạnh bằng 2a), \(SN=\frac{1}{2}A'C=\frac{1}{2}.2\sqrt{2}a=\sqrt{2}a\) (vì \(\Delta SA'C\) vuông tại S)

\(\Delta SMN\) vuông tại N, \(NH\bot SM\Rightarrow \frac{1}{N{{H}^{2}}}=\frac{1}{S{{N}^{2}}}+\frac{1}{M{{N}^{2}}}=\frac{1}{2{{a}^{2}}}+\frac{1}{{{a}^{2}}}=\frac{3}{2{{a}^{2}}}\Rightarrow NH=\frac{a\sqrt{6}}{3}\)

\(\Rightarrow d\left( A;\left( SBC \right) \right)=\frac{a\sqrt{6}}{3}\)

Chọn: B