Phương pháp giải:

+) Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ \(x = {x_0}\)

+) Thay tọa độ điểm A vào phương trình, tìm điều kiện của m để phương trình có 3 nghiệm \({x_0}\).

Lời giải chi tiết:

Ta có : \(y' = 3{x^2} - 6x\).

\( \Rightarrow \) Phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ \(x = {x_0}\) là :

\(\begin{array}{l}y = \left( {3x_0^2 - 6{x_0}} \right)\left( {x - {x_0}} \right) + x_0^3 - 3x_0^2\,\,\left( d \right)\\A \in \left( d \right) \Rightarrow m = \left( {3x_0^2 - 6{x_0}} \right)\left( {2 - {x_0}} \right) + x_0^3 - 3x_0^2\\ \Leftrightarrow m = 6x_0^2 - 3x_0^3 - 12{x_0} + 6x_0^2 + x_0^3 - 3x_0^2\\ \Leftrightarrow 2x_0^3 - 9x_0^2 + 12{x_0} =  - m\,\,\left( * \right)\end{array}\)

Để từ A kẻ được 3 tiếp tuyến đến đồ thị hàm số \(y = {x^3} - 3{x^2}\) thì phương trình (*) có 3 nghiệm phân biệt.

Xét hàm số \(f\left( x \right) = 2{x^3} - 9{x^2} + 12x\) ta có : \(f'\left( x \right) = 6{x^2} - 18x + 12 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 2\\x = 1\end{array} \right.\) .

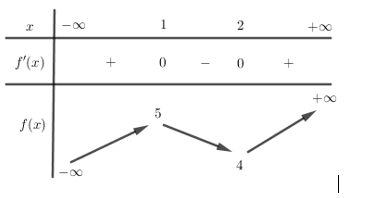
BBT :

Để phương trình (*) có 3 nghiệm phân biệt \( \Rightarrow \) đường thẳng \(y =  - m\) cắt đồ thị hàm số \(y = f\left( x \right)\) tại 3 điểm phân biệt \( \Rightarrow 4 <  - m < 5 \Leftrightarrow  - 5 < m <  - 4\).

Chọn C.