Câu hỏi
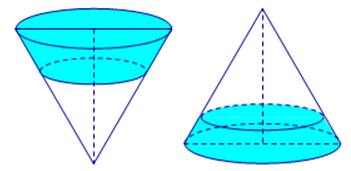
Một cái phễu có dạng hình nón, chiều cao của phễu là \(20\,\text{cm}\). Người ta đổ một lượng nước vào phễu sao cho chiều cao của cột nước trong phễu bằng \(10\,\text{cm}\) (hình H1). Nếu bịt kín miệng phễu rồi lật ngược phễu lên (hình H2) thì chiều cao của cột nước trong phễu gần bằng với giá trị nào sau đây?
- A \(0,87\,\text{cm}\).
- B \(10\,\text{cm}\).
- C \(1,07\,\text{cm}\).
- D \(1,35\,\text{cm}\).
Phương pháp giải:
Sử dụng tỉ lệ thể tích để tìm chiều cao của cột nước trong phễu
Lời giải chi tiết:
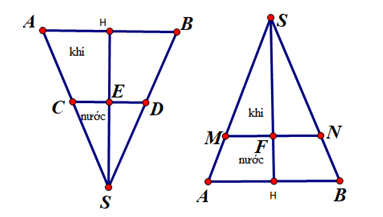
Hình vẽ tham khảo
Trước khi lật phễu lên: Theo bài ra ta có \(SE=10\text{cm}\), \(SH=20\text{cm}\). \(\Delta SCD\backsim \Delta SAB\Rightarrow \frac{1}{2}=\frac{SE}{SH}=\frac{ED}{HB}\)
Suy ra \(\frac{{{V}_{nuoc}}}{{{V}_{pheu}}}=\frac{E{{D}^{2}}.SE}{H{{B}^{2}}.SH}=\frac{1}{8}\Rightarrow {{V}_{khi}}=\frac{7}{8}{{V}_{pheu}}\).
Sau khi lật phễu lên: Tam giác \(\Delta SMN\,\,\sim \,\,\Delta SAB\Rightarrow \frac{SF}{SH}=\frac{FN}{HB}\)
Do \({{V}_{khi}}=\frac{7}{8}{{V}_{pheu}}\Leftrightarrow {{\left( \frac{FN}{HB} \right)}^{2}}.\frac{SF}{SH}=\frac{7}{8}\Leftrightarrow {{\left( \frac{SF}{SH} \right)}^{3}}=\frac{7}{8}\Leftrightarrow SF=\frac{\sqrt[3]{7}}{2}SH\).
Vậy chiều cao cần tính là \(FH=SH-SF=SH\left( 1-\frac{\sqrt[3]{7}}{2} \right)=20.\left( 1-\frac{\sqrt[3]{7}}{2} \right)\approx 0,8706\).
Chọn A