Câu hỏi
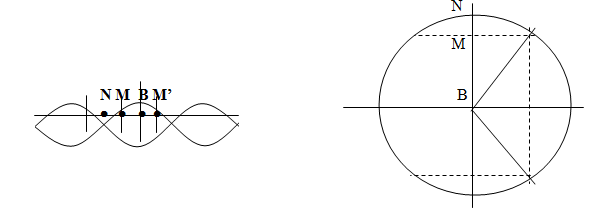
Trên 1 dây có sóng dừng,bề rộng của bụng sóng là 4a thì khoảng cách gần nhất dao động với biên độ bằng a là bao nhiêu (lamda) ?
Lời giải chi tiết:
Khoảng cách giữa hai điểm liền kề có biên độ a có thể là 2BM hoặc 2MN
Phương trình sóng dừng tại M cách nút N một khoảng d
\(u = 2a\cos (\frac{{2\pi d}}{\lambda } + \frac{\pi }{2})\cos (\omega t - \frac{\pi }{2})\)
AM = 2a cos(\(\frac{{2\pi d}}{\lambda }\)+\(\frac{\pi }{2}\)) = a -----> cos(\(\frac{{2\pi d}}{\lambda }\)+\(\frac{\pi }{2}\)) = \(\frac{1}{2}\)
-----> \(\frac{{2\pi d}}{\lambda }\)+\(\frac{\pi }{2}\) = ±\(\frac{\pi }{3}\) + kp----> d = (±\(\frac{1}{3}\) - \(\frac{1}{2}\) +\(\frac{k}{2}\))l
-------> d1 = (-\(\frac{1}{3}\) - \(\frac{1}{2}\) +\(\frac{{2 + {n_1}}}{2}\))l ----->d1 = \(\frac{\lambda }{6}\) + n1\(\frac{\lambda }{2}\)
-------> d2 = (\(\frac{1}{3}\) - \(\frac{1}{2}\) +\(\frac{{1 + {n_2}}}{2}\))l ----->d2 = \(\frac{\lambda }{3}\) + n2\(\frac{\lambda }{2}\)
d1min = NM = \(\frac{\lambda }{6}\)----> 2MN = \(\frac{\lambda }{3}\)
d2min = NM’ = NM + 2 MB = \(\frac{\lambda }{3}\)-----> MM’.= 2MB = \(\frac{\lambda }{3}\) - \(\frac{\lambda }{6}\) = \(\frac{\lambda }{6}\)
Do đó khoảng cách ngắn nhất giữa hai điểm dao động với biên độ a là MM’ = \(\frac{\lambda }{6}\); hai điểm này thuộc cùng một bó sóng