Câu hỏi
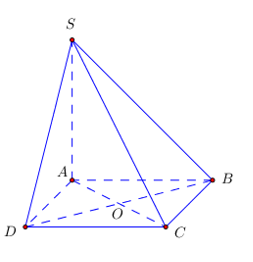
Chóp SBCD. CB = CD = a. \(SC = a\sqrt 3 ,\,\,SB = a\sqrt 2 ;\,\,\widehat {BCD} = {90^0}\). Tính \(\widehat {\left( {\left( {SBC} \right);\left( {BCD} \right)} \right)}\) biết \(SC \bot BD\).
- A \({30^0}\)
- B \({45^0}\)
- C \({60^0}\)
- D \({90^0}\)
Lời giải chi tiết:
* Lấy O là trung điểm của BD. Dựng A đối xứng với C qua O.
\(\Delta BCD\) vuông cân tại \(A \Rightarrow ABCD\) là hình vuông.
* \(\Delta SBC\) có \(S{C^2} = S{B^2} + B{C^2} \Rightarrow \Delta SBC\) vuông ở B.
* \(\left\{ \begin{array}{l}CB \bot AB\\CB \bot SB\end{array} \right. \Rightarrow CB \bot \left( {SAB} \right) \Rightarrow CB \bot SA\,\,\left( 1 \right)\)
* \(\left\{ \begin{array}{l}BD \bot AC\\BD \bot SC\end{array} \right. \Rightarrow BD \bot \left( {SAC} \right) \Rightarrow BD \bot SA\,\,\left( 2 \right)\)
Từ (1) và (2) \( \Rightarrow SA \bot \left( {ABCD} \right)\).
\( \Rightarrow \widehat {\left( {\left( {SBC} \right);\left( {BCD} \right)} \right)} = \widehat {\left( {\left( {SBC} \right);\left( {ABCD} \right)} \right)} = \widehat {SBA} = {45^0}\)
Chọn đáp án B.