Phương pháp giải:

sử dụng phương pháp vecto quay, biến đổi bài toán năng lượng thành bài toán tọa độ

Lời giải chi tiết:

Áp dụng định luật bảo toàn cơ năng: khi động năng là 3J thì thế năng là 1J và khi động năng là 3,6J thì thế năng là 0,4J.

Ta có:

\(\begin{array}{l}
\frac{1}{2}.k.x_1^2 = 1J = \frac{1}{4}.{\rm{W}} = \frac{1}{4}.\frac{1}{2}.k.{A^2}\\
= > {x_1} = \pm \frac{A}{2}cm\\
\frac{1}{2}.k.x_2^2 = 0,4J = \frac{1}{{10}}.{\rm{W}} = \frac{1}{{10}}.\frac{1}{2}.k.{A^2}\\
= > {x_1} = \pm \frac{A}{{\sqrt {10} }}cm
\end{array}\)

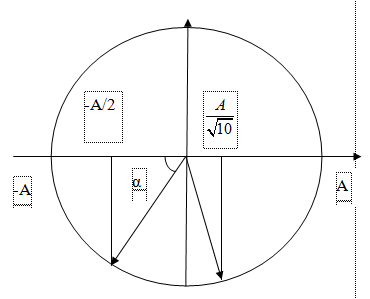
Ta có đường tròn

Do tính đối xứng nên ta chỉ cần xét trường hợp như trong hình.

\(\begin{array}{l}
\cos \alpha = \frac{1}{2} = > \alpha = {60^0}\\
\cos \beta = \frac{1}{{\sqrt {10} }} = > \beta = {71^0}33'
\end{array}\)

Vậy góc quét của OM là :

\(\begin{array}{l}
\varphi = 180 - 60 - 71,5 = 48,{5^0}\\
= > \Delta t = \frac{\varphi }{{360}}.T \approx 0,41s
\end{array}\)