Câu hỏi
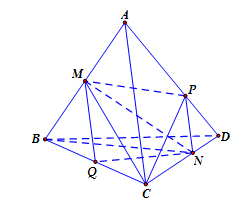
Cho tứ diện đều \(ABCD\) có cạnh bằng \(1\). Trên các cạnh \(AB\) và \(CD\) lần lượt lấy các điểm \(M\) và \(N\) sao cho \(\overrightarrow{MA}+\overrightarrow{MB}=\overrightarrow{0}\) và \(\overrightarrow{NC}=-2\overrightarrow{ND}\). Mặt phẳng \(\left( P \right)\) chứa \(MN\) và song song với \(AC\) chia khối tứ diện \(ABCD\) thành hai khối đa diện, trong đó khối đa diện chứa đỉnh \(A\) có thể tích là \(V\). Tính \(V\).
- A \(V=\frac{\sqrt{2}}{18}\).
- B \(V=\frac{11\sqrt{2}}{216}\).
- C \(V=\frac{7\sqrt{2}}{216}\).
- D \(V=\frac{\sqrt{2}}{108}\).
Phương pháp giải:
Xác định mặt phẳng thiết diện, chia nhỏ các khối đa diện và áp dụng công thức tỉ số thể tích
Lời giải chi tiết:
Từ \(N\) kẻ \(NP\text{//}AC\), \(N\in AD\).
Qua \(M\) kẻ \(MQ\text{//}AC\), \(Q\in BC\). Mặt phẳng \(\left( P \right)\) là \(MPNQ\)
Ta có \({{V}_{ABCD}}=\frac{1}{3}AH.{{S}_{ABCD}}=\frac{\sqrt{2}}{12}\) và \(V={{V}_{ACMPNQ}}={{V}_{AMPC}}+{{V}_{MQNC}}+{{V}_{MPNC}}\)
Lại có \({{V}_{AMPC}}=\frac{AM}{AB}.\frac{AP}{AD}.{{V}_{ABCD}}\)\(=\frac{1}{2}.\frac{2}{3}{{V}_{ABCD}}=\frac{1}{3}{{V}_{ABCD}}\) \({{V}_{MQNC}}=\frac{1}{2}{{V}_{AQNC}}=\frac{1}{2}\frac{CQ}{CB}.\frac{CN}{CD}.{{V}_{ABCD}}\)\(=\frac{1}{2}\frac{1}{2}.\frac{2}{3}{{V}_{ABCD}}=\frac{1}{2}{{V}_{ABCD}}\) \({{V}_{MPNC}}=\frac{2}{3}{{V}_{MPCD}}=\frac{2}{3}.\frac{1}{3}{{V}_{MACD}}\)\(=\frac{2}{3}.\frac{1}{3}\frac{AM}{AB}.{{V}_{ABCD}}\)\(=\frac{2}{3}.\frac{1}{3}\frac{1}{2}{{V}_{ABCD}}=\frac{1}{9}{{V}_{ABCD}}\)
Vậy \(V=\left( \frac{1}{3}+\frac{1}{6}+\frac{1}{9} \right){{V}_{ABCD}}\)\(\Rightarrow V=\frac{11}{18}{{V}_{ABCD}}=\frac{11\sqrt{2}}{216}\).
Chọn B