Câu hỏi
Một sóng cơ truyền trên một sợi dây rất dài từ một đầu dây với biên độ không đổi là 4 mm, tốc độ truyền sóng trên dây là 2,4 m/s, tần số sóng là 20 Hz. Hai điểm M và N trên dây cách nhau 37 cm, sóng truyền từ M đến N. Tại thời điểm t, sóng tại M có li độ -2 mm và M đang đi về vị trí cân bằng. Vận tốc dao động của điểm N ở thời điểm (t -\({{89} \over {80}}\) ) s là
- A 16π cm/s.
- B \(- 8\sqrt 3 \pi {\rm{ }}cm/s.\)
- C \(80\sqrt 3 \pi {\rm{ }}mm/s.\)
- D -8π cm/s.
Lời giải chi tiết:
Đáp án B
Ta có : \(\lambda = {v \over f} = 12cm = > MN = 37cm = 3\lambda + {\lambda \over {12}}\)
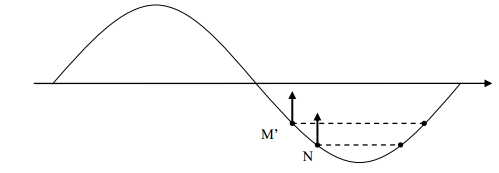
Vì sóng tuần hoàn theo không gian nên sau điểm M đoạn 3λ có điểm M’ có tính chất như điểm M
nên ở thời điểm t điểm M’ cũng có li độ uM’= -2 mm và đang đi về VTCB.
Vì \({u_{M'}} = - 2mm = - {A \over 2} = > {x_{M'}} = {\lambda \over {12}}\)
Vì N cách M’ đoạn \({\lambda \over {12}} = > {x_N} = {\lambda \over 6}\)
Ta có : \(\Delta t = {{89} \over {80}}s = 22T + {T \over 4}\)=> lùi về quá khứ \({T \over 4}\)=> điểm N có li độ \({x_N} = - {A \over 2}\)
\({v_N} = - {{\omega A\sqrt 3 } \over 2} = - 80\pi \sqrt 3 (mm/s)\)