Câu hỏi
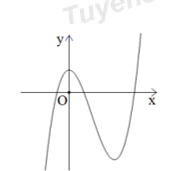
Đường cong trong hình bên là đồ thị của hàm số nào dưới đây?
- A
\(y=-{{x}^{3}}+3{{x}^{2}}+1\).
- B
\(y=-{{x}^{3}}-3{{x}^{2}}+1\).
- C
\(y={{x}^{3}}+3{{x}^{2}}+1\).
- D \(y={{x}^{3}}-3{{x}^{2}}+1\).
Phương pháp giải:
Nhận dạng đồ thị các hàm số hàm số bậc ba.
Lời giải chi tiết:
Ta thấy, khi \(x\to +\infty \) thì \(y\to +\infty \,\,\,\Rightarrow \) Hàm số bậc ba \(y=a{{x}^{3}}+b{{x}^{2}}+cx+d\) có a > 0.
\(\Rightarrow \) Loại bỏ phương án A và B.
Quan sát đồ thị ta thấy hàm số đạt cực trị tại \({{x}_{1}}=0,\,\,{{x}_{2}}>0\).
Xét hàm số \(y={{x}^{3}}+3{{x}^{2}}+1\Rightarrow y'=3{{x}^{2}}+6x,\,\,y'=0\Leftrightarrow \left[ \begin{align} x=0 \\ x=-2<0 \\ \end{align} \right.\)
\(\Rightarrow \) Loại bỏ phương án C.
Chọn phương án D.
Chọn: D