Câu hỏi
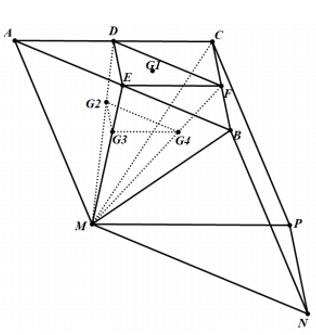
Cho lăng trụ tam giác ABC.MNP có thể tích V. Gọi \({{G}_{1}};{{G}_{2}};{{G}_{3}};{{G}_{4}}\) lần lượt là trọng tâm của các tam giác ABC, ACM, AMB, BCM, \({{V}_{1}}\) là thể tích của khối tứ diện \({{G}_{1}}{{G}_{2}}{{G}_{3}}{{G}_{4}}\). Khẳng định nào sau đây là đúng?
- A
\(V=27{{V}_{1}}\)
- B
\(V=9{{V}_{1}}\)
- C
\(V=81{{V}_{1}}\)
- D \(8V=81{{V}_{1}}\)
Phương pháp giải:
So sánh diện tích đáy và chiều cao của các khối chóp.
Lời giải chi tiết:
Gọi D, E, F lần lượt là trung điểm của AC, AB, BC.
Vì \({{G}_{2}};{{G}_{3}};{{G}_{4}}\) là trọng tâm các tam giác MAC, MAB, MBC nên
\(\begin{align} {{G}_{2}}\in MD;M{{G}_{2}}=2D{{G}_{2}} \\ {{G}_{3}}\in ME;M{{G}_{3}}=2E{{G}_{3}} \\ {{G}_{4}}\in MF;M{{G}_{4}}=2F{{G}_{4}} \\ \Rightarrow \left( {{G}_{2}}{{G}_{3}}{{G}_{4}} \right)//\left( DEF \right) \\ \Rightarrow {{V}_{1}}={{V}_{E.{{G}_{2}}{{G}_{3}}{{G}_{4}}}}=\frac{E{{G}_{3}}}{M{{G}_{3}}}.{{V}_{M.{{G}_{2}}{{G}_{3}}{{G}_{4}}}}=\frac{1}{2}{{V}_{M.{{G}_{2}}{{G}_{3}}{{G}_{4}}}} \\ \end{align}\)
Lại có \(\frac{{{V}_{M.{{G}_{2}}{{G}_{3}}{{G}_{4}}}}}{{{V}_{MDEF}}}=\frac{M{{G}_{2}}.M{{G}_{3}},M{{G}_{4}}}{MD.ME.MF}=\frac{2}{3}.\frac{2}{3}.\frac{2}{3}=\frac{8}{27}\)
\(\Rightarrow {{V}_{1}}=\frac{1}{2}.\frac{8}{27}{{V}_{MDEF}}=\frac{4}{27}{{V}_{MDEF}}\)
Lại có \({{S}_{DEF}}=\frac{1}{4}{{S}_{ABC}}\Rightarrow {{V}_{M.DEF}}=\frac{1}{4}{{V}_{M.ABC}}=\frac{1}{4}.\frac{1}{3}V=\frac{V}{12}\)
Vậy \({{V}_{1}}=\frac{4}{27}.\frac{V}{12}==\frac{V}{81}\).
Chọn C.