Câu hỏi
Một sợi dây đàn hồi căng ngang, đang có sóng dừng ổn định. Trên dây, A là một điêm nút, B là một điểm bụng gần A nhất với AB = 18cm. M là một điểm trên dây cách B một khoảng 12cm. Biết rằng trong một chu kì sóng, khoảng thời gian mà độ lớn vận tốc dao động của phần tử B nhỏ hơn vận tốc cực đại của phần tử M là 0,1s. Tốc độ truyền sóng trên dây là
- A 5,6m/s
- B 4,8m/s
- C 2,4m/s
- D 3,2m/s
Phương pháp giải:
Sử dụng đường tròn lượng giác
Lời giải chi tiết:
A là điểm nút, B là điểm bụng gần A nhất => AB = λ/4 = 18cm => λ = 72cm
M là một điểm trên dây cách B một khoảng 12cm => M cách nút gần nó nhất một khoảng 6cm
=> Biên độ dao động tại M: \({A_M} = \left| {2a\sin {{2\pi .6} \over {72}}} \right| = a \Rightarrow {v_{M\max }} = \omega {A_M} = \omega a\)
Vận tốc cực đại của phần tử B: vBmax = ω.2A
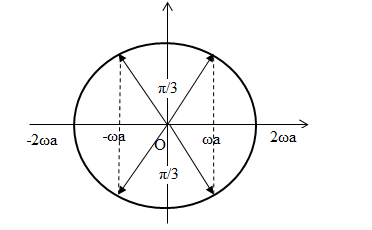
Biểu diễn trên đường tròn lượng giác của vận tốc:
\(\eqalign{
& \Rightarrow \alpha = {\pi \over 3} + {\pi \over 3} = {{2\pi } \over 3} \Rightarrow \Delta t = \alpha {T \over {2\pi }} = {{2\pi } \over 3}{T \over {2\pi }} = {T \over 3} = 0,1s \Rightarrow T = 0,3s \cr
& \Rightarrow v = {\lambda \over T} = {{72} \over {0,3}} = 2,4m/s \cr} \)