Phương pháp giải:

 Lập phương trình tiếp tuyến với hệ số góc k và đi qua điểm thuộc Oy, sử dụng điều kiện để hai đồ thị tiếp xúc tìm tham số m 

Lời giải chi tiết:

 Gọi \(M\left( 0;m \right)\in Oy\)\(\Rightarrow \)

Phương trình tiếp tuyến của \(\left( C \right)\) có dạng \(\left( d \right):y=kx+m.\) Vì \(\left( C \right)\) tiếp xúc với \(\left( d \right)\)\(\Rightarrow \)\(\left\{ \begin{align} & 4{{x}^{3}}-8x=k \\ & {{x}^{4}}-4{{x}^{2}}+3=kx+m \\ \end{align} \right.\Leftrightarrow {{x}^{4}}-4{{x}^{2}}+3=\left( 4{{x}^{3}}-8x \right)x+m\) \(\Leftrightarrow m=\underbrace{-\,3{{x}^{4}}+4{{x}^{2}}+3}_{f\left( x \right)}.\)

Yêu cầu bài toán \(\Leftrightarrow \,\,m=f\left( x \right)\) có 3 nghiệm phân biệt.

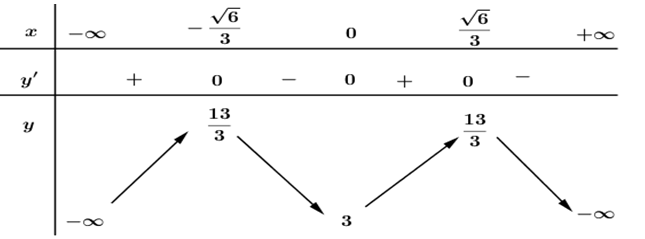
Xét hàm số \(f\left( x \right)=-\,3{{x}^{4}}+4{{x}^{2}}+3\) trên \(\mathbb{R},\) có \({f}'\left( x \right)=-\,12{{x}^{3}}+8x;\,\,{f}'\left( x \right)=0\Leftrightarrow \left[ \begin{align} & x=0 \\ & x=\pm \,\frac{\sqrt{6}}{3} \\ \end{align} \right..\)

Ta có BBT:

Dựa vào bảng biến thiên, để \(m=f\left( x \right)\) có 3 nghiệm phân biệt \(\Leftrightarrow \,\,m=3.\)

Vậy có duy nhất 1 điểm \(M\in Oy\) thỏa mãn yêu cầu bài toán.

Chọn C