Câu hỏi
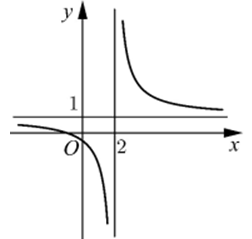
Đường cong của hình vẽ bên là đồ thị của hàm số \(y=\frac{ax+b}{cx+d}\) với \(a,\,\,b,\,\,c,\,\,d\) là các số thực.
Mệnh đề nào sau đây là đúng ?
- A \({y}'>0,\,\,\forall x\ne 1.\)
- B \({y}'>0,\,\,\forall x\ne 2.\)
- C \({y}'<0,\,\,\forall x\ne 1.\)
- D \({y}'<0,\,\,\forall x\ne 2.\)
Phương pháp giải:
Dựa vào hình dáng, đường tiệm cận đồ thị hàm số
Lời giải chi tiết:
Dựa vào hình vẽ, ta thấy đồ thị hàm số có tiệm cận đứng \(x=2\) và đi xuống.
Vậy hàm số nghịch biến trên khoảng \(\left( -\,\infty ;2 \right)\) và \(\left( 2;+\,\infty \right)\)\(\Rightarrow \)\({y}'<0,\,\,\forall x\ne 2.\)
Chọn D
Câu hỏi trước
