Câu hỏi
Một quân vua được đặt trên một ô giữa bàn cờ vua. Mỗi bước di chuyển, quân vua được di chuyển sang một ô khác chung cạnh hoặc chung đỉnh với ô đang đứng (xem hình minh họa). Bạn An di chuyển quân vua ngẫu nhiên 3 bước. Tính xác suất sau 3 bước quân vua trở về đúng ô xuất phát.
- A \(\frac{1}{16}\)
- B \(\frac{1}{32}\)
- C \(\frac{3}{32}\)
- D \(\frac{3}{64}\)
Phương pháp giải:
Quân vua được di chuyển sang một ô khác chung cạnh hoặc chung đỉnh với ô đang đứng \(\Rightarrow \left| \Omega \right|\).
Gọi A là biến cố : « Quân vua sau 3 bước trở về đúng vị trí ban đầu » . Tính \(\left| A \right|\). \(\Rightarrow P\left( A \right)=\frac{\left| A \right|}{\left| \Omega \right|}\).
Lời giải chi tiết:
Quân vua được di chuyển sang một ô khác chung cạnh hoặc chung đỉnh với ô đang đứng \(\Rightarrow \left| \Omega \right|={{8}^{3}}\).
Gọi A là biến cố : « Quân vua sau 3 bước trở về đúng vị trí ban đầu »
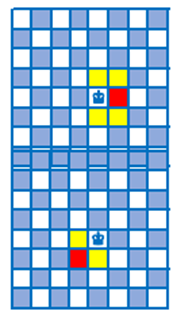
TH1: Quân vua di chuyển bước thứ nhất sang ô đen liền kề (được tô màu đỏ) có 4 cách.
Bước đi thứ 2 quân vua di chuyển sang các ô được tô màu vàng có 4 cách.
Bước đi thứ 3 quay về vị trí ban đầu có 1 cách.
Vậy TH này có 4.4 = 16 cách.
TH2: Quân vua di chuyển bước thứ nhất sang các ô trắng liền kề (được tô màu đỏ) có 4 cách.
Bước đi thứ 2 quân vua di chuyển sang các ô được tô màu vàng có 2 cách.
Bước đi thứ 3 quay về vị trí ban đầu có 1 cách.
Vậy TH này có 4.2 = 8 cách.
\(\begin{align} & \Rightarrow \left| A \right|=8.3=24 \\ & \Rightarrow P\left( A \right)=\frac{24}{{{8}^{3}}}=\frac{3}{64} \\ \end{align}\)
Chọn D.