Câu hỏi
Cho hình nón có góc ở đỉnh bằng \({{60}^{0}},\) bán kính đáy bằng \(a.\) Diện tích xung quanh của hình nón bằng:
- A \(2\pi {{a}^{2}}\)
- B \(\pi {{a}^{2}}\)
- C \(\pi {{a}^{2}}\sqrt{3}\)
- D \(4\pi {{a}^{2}}\)
Phương pháp giải:
+) Thiết diện qua trục của hình nón luôn là tam giác cân tại đỉnh của hình nón.
+) Diện tích xung quanh của hình nón bán kính \(R\) và đường sinh \(l\) là: \(S=\pi Rl.\)
Lời giải chi tiết:
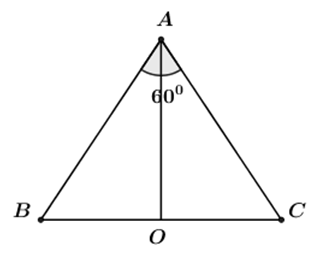
Giả sử thiết diện qua trục của hình nón là tam giác \(ABC\) có \(\widehat{BAC}={{60}^{0}}.\) \(\Rightarrow \Delta ABC\) là tam giác đều
Gọi \(O\) là trung điểm của \(BC\Rightarrow O\) là tâm của đường tròn đáy.
\(\begin{align} & \Rightarrow BC=2.OB=2R=2a. \\ & \Rightarrow l=AB=AC=BC=2a. \\ & \Rightarrow {{S}_{xq}}=\pi Rl=\pi .a.2a=2\pi {{a}^{2}}. \\ \end{align}\)
Chọn A.
Câu hỏi trước
