Câu hỏi
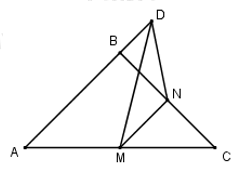
Cho hình chóp S.ABC có \(SA=SB=SC=3\), tam giác ABC vuông cân tại B và \(AC=2\sqrt{2}\). Gọi M, N lần lượt là trung điểm của AC, BC. Trên 2 cạnh SA, SB lấy các điểm P, Q tương ứng sao cho SP = 1, SQ = 2. Tính thể tích V của khối tứ diện MNPQ.
- A
\(V=\frac{\sqrt{3}}{12}\).
- B
\(V=\frac{\sqrt{34}}{12}\).
- C
\(V=\frac{\sqrt{7}}{18}\).
- D \(V=\frac{\sqrt{34}}{144}\).
Phương pháp giải:
Sử dụng công thức tỉ số thể tích.
Lời giải chi tiết:
Trong (SAB), kéo dài PQ cắt AB tại D.
Áp dụng định lí Menelaus trong tam giác SAB có \(\frac{PS}{PA}.\frac{DA}{DB}.\frac{QB}{QS}=1\Leftrightarrow \frac{1}{2}.\frac{DA}{DB}.\frac{1}{2}=1\Leftrightarrow \frac{DA}{DB}=4\Rightarrow \frac{BA}{BD}=3\)
Áp dụng định lí Menelaus trnong tam giác ADP có: \(\frac{BA}{BD}.\frac{QD}{DP}.\frac{SP}{SA}=1\Leftrightarrow 3.\frac{QD}{DP}.\frac{1}{3}=1\Leftrightarrow \frac{QD}{DP}=1\)
\(\Rightarrow\frac{{{V}_{PQMN}}}{{{V}_{PDMN}}}=\frac{PQ}{PD}=\frac{1}{2}\Rightarrow {{V}_{PQMN}}=\frac{1}{2}{{V}_{PDMN}}\)
Ta có:
\(\begin{align} {{S}_{DMN}}=\frac{1}{2}d\left( D;MN \right).MN=\frac{1}{2}d\left( C;MN \right).MN=\frac{1}{2}.\frac{1}{2}d\left( C;AB \right).\frac{1}{2}AB \\ \,\,\,\,\,\,\,\,\,\,\,\,=\frac{1}{4}.\frac{1}{2}d\left( C;AB \right).AB=\frac{1}{4}{{S}_{ABC}} \\ \end{align}\)
\(\begin{align} \frac{d\left( P;\left( DMN \right) \right)}{d\left( S;\left( ABC \right) \right)}=\frac{PA}{SA}=\frac{2}{3} \\ \Rightarrow \frac{{{V}_{P.DMN}}}{{{V}_{S.ABC}}}=\frac{2}{3}.\frac{1}{4}=\frac{1}{6}\Rightarrow {{V}_{P.DMN}}=\frac{1}{6}{{V}_{S.ABC}} \\ \Rightarrow {{V}_{PQMN}}=\frac{1}{12}{{V}_{S.ABC}} \\ \end{align}\)
Ta có \(BA=BC=\frac{AC}{\sqrt{2}}=\frac{2\sqrt{2}}{\sqrt{2}}=2\Rightarrow {{S}_{ABC}}=\frac{1}{2}A{{B}^{2}}=2\)
Xét tam giác vuông SAM có \(SM=\sqrt{S{{A}^{2}}-A{{M}^{2}}}=\sqrt{9-2}=\sqrt{7}\)
\(\begin{align} \Rightarrow {{V}_{S.ABC}}=\frac{1}{3}SM.{{S}_{ABC}}=\frac{1}{3}\sqrt{7}.2=\frac{2\sqrt{7}}{3} \\ \Rightarrow {{V}_{PQMN}}=\frac{1}{12}{{V}_{S.ABC}}=\frac{\sqrt{7}}{18} \\ \end{align}\)
Chọn: C.