Câu hỏi
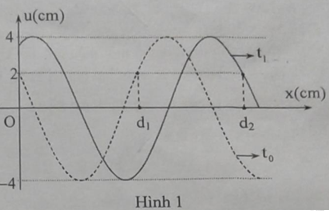
Cho một sóng cơ truyền dọc theo trục Ox trên một sợi dây đàn hồi rất dài chu ỳ 6s. Tại thời điểm t0 = 0 và thời điểm t1 = 1,75s, hình dạng sợi dây như hình 1. Biết d2 – d1 = 3cm. Tỉ số giữa tốc độ dao đọng cự đại của phần tử trên dây và tốc độ truyền sóng là
- A 2π
- B \(\frac{{5\pi }}{3}\)
- C \(\frac{{5\pi }}{8}\)
- D \(\frac{{3\pi }}{4}\)
Lời giải chi tiết:
Đáp án B
Ta có \(\omega = \frac{{2\pi }}{T} = \frac{{2\pi }}{6} = \frac{\pi }{3}(rad/s)\)
Gọi s là quãng đường sóng truyền được trong thời gian 1,75s
Từ hình vẽ ta có \(\frac{\lambda }{6} + s + \frac{\lambda }{6} = 3\)
Mặt khác ta có\(t = 1,75s = \frac{{7T}}{{24}} = > s = \frac{{7\lambda }}{{24}} = > \frac{\lambda }{6} + \frac{{7\lambda }}{{24}} + \frac{\lambda }{6} = 3 = > \lambda = 4,8cm\)
Tốc độ truyền sóng là \(v = \frac{\lambda }{T} = \frac{{4,8}}{6} = 0,8(cm/s)\)
Tốc độ dao động cực đại là\({v_{max}} = \omega A = \frac{\pi }{3}.4 = \frac{{4\pi }}{3}(cm/s)\)
Tỷ số giữa tốc độ dao động cực đại và tốc độ truyền sóng trên dây là \(\frac{{\frac{{4\pi }}{3}}}{{0,8}} = \frac{{5\pi }}{3}\)







