Câu hỏi
Cho đoạn mạch AB gồm cuộn dây thuần có điện trở thuần 100Ω và độ tự cảm \(\frac{1}{\pi }H\)mắc nối tiếp với tụ điện có điện dung \(\frac{{{{10}^{ - 4}}}}{{2\pi }}F\). Đặt vào hai đầu đoạn mạch AB một điện áp xoay chiều \({u_{AB}} = 200\cos 100\pi t(V)\). Khi điện áp tức thời giữa hai đầu đoạn mạch AB là\(100\sqrt 3 V\) và đang giảm thì điện áp tức thới giữa hai đầu cuộn dây là
- A -100 V và đang giảm
- B – 100 V và đang tăng
- C 100 V và đang giảm
- D 100 V và đang tăng
Lời giải chi tiết:
Đáp án A
Tổng trở của mạch là \(Z = \sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} = \sqrt {{{100}^2} + \left( {100\pi .\frac{1}{\pi } - \frac{1}{{\frac{{{{10}^{ - 4}}.100\pi }}{{2\pi }}}}} \right)} = 100\sqrt 2 \Omega \)
Độ lệch pha giữa u và i được xác định bởi biểu thức \(\tan \varphi = \frac{{{Z_l} - {Z_C}}}{R} = \frac{{100 - 200}}{{100}} = - 1 = > \varphi = - \frac{\pi }{4}\)
Biểu thức cường độ dòng điện \(i = \sqrt 2 \cos \left( {100\pi t - \frac{\pi }{4}} \right)A\)
Độ lệch pha giữa ud và i được xác định bởi biểu thức \(\tan {\varphi _d} = \frac{{{Z_L}}}{R} = \frac{{100}}{{100}} = 1 = > {\varphi _d} = \frac{\pi }{4}\)
Biểu thức điện áp hai đầu cuộn dây là \({u_d} = \sqrt {{R^2} + Z_L^2} .{I_0}\cos \left( {100\pi t + \frac{\pi }{2}} \right) = 200\cos (100\pi t + \frac{\pi }{2})\)
Tại thời điểm t:
\(\eqalign{
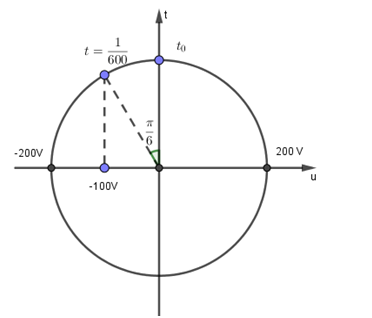
& {u_{AB}} = 100\sqrt 3 = 200\cos 100\pi t = > t = {1 \over {600}}s \cr
& = > {u_d} = 200\cos \left( {100\pi t + {\pi \over 2}} \right) = 200\cos \left( {100\pi {1 \over {600}} + {\pi \over 2}} \right) = - 100V \cr} \)
Ta có \(t = \frac{1}{{600}}s \Leftrightarrow \frac{T}{{12}} \Leftrightarrow \frac{\pi }{6}\) biểu diễn trên đường tròn lượng giác ta thấy điện áp ở hai đầu cuộn dây đang giảm