Câu hỏi
Một vật dao động điều hòa với biên độ A và chu kỳ T. Trong khoảng thời gian ∆t = 5T/6, quãng đường nhỏ nhất (Smin) mà vật đi được là
- A A\(\root \of 3 \)
- B A + A\(\root \of 3 \)
- C 2A + A\(\root \of 3 \)
- D 3A.
Phương pháp giải:
Sử dụng đường tròn lượng giác
Lời giải chi tiết:
Ta có: \(\Delta t = {{5T} \over 6} = {T \over 2} + {T \over 3} \Rightarrow {S_{\min }} = 2A + {S_{\min T/3}}\)
=> Góc quét được trong khoảng thời gian T/3 là 2π/3.
Quãng đường vật đi được trong ½ chu kì là 2A.
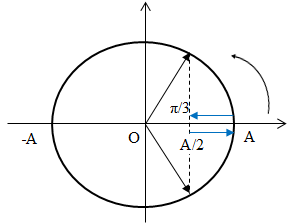
+ Vật có v = 0 khi qua vị trí biên => Trong cùng một khoảng thời gian vật đi được quãng đường nhỏ nhất khi đi xung quanh vị trí biên. Biểu diễn trên đường lượng giác ta có:
\( \Rightarrow {S_{\min {\rm{T/3}}}} = {A \over 2} + {A \over 2} = A \Rightarrow {S_{\min }} = 2A + {S_{\min T/3}} = 2A + A = 3A\)
Câu hỏi trước
