Câu hỏi
Một vật dao động điều hòa với biên độ A và chu kỳ T. Trong khoảng thời gian ∆t = 3T/4, quãng đường lớn nhất (Smax) mà vật đi được là
- A 2A - A\(\root \of 2 \).
- B 2A + A\(\root \of 2 \).
- C 2A\(\root \of 3 \).
- D A + A\(\root \of 2 \).
Phương pháp giải:
Sử dụng đường tròn lượng giác
Lời giải chi tiết:
Ta có: \(\Delta t = {{3T} \over 4} = {T \over 2} + {T \over 4} \Rightarrow {S_{m{\rm{ax}}}} = 2A + {S_{\max T/4}}\)
=> Góc quét được trong khoảng thời gian T/4 là π/2.
Quãng đường vật đi được trong ½ chu kì là 2A.
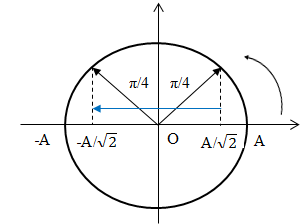
Vật có tốc độ cực đại khi qua vị trí cân bằng. Trong cùng một khoảng thời gian vật đi được quãng đường lớn nhất khi đi xung quanh vị trí cân bằng. Biểu diễn trên đường tròn lượng giác:
\( \Rightarrow {S_{m{\rm{axT/4}}}} = {5 \over {\sqrt 2 }} + {5 \over {\sqrt 2 }} = 5\sqrt 2 cm \Rightarrow {S_{m{\rm{ax}}}} = 2A + {S_{\max T/4}} = 2A + {A \over {\sqrt 2 }} + {A \over {\sqrt 2 }} = 2A + A\sqrt 2 \)