Câu hỏi
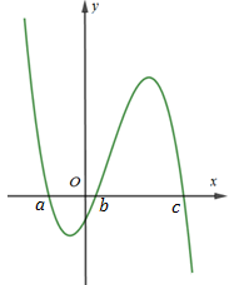
Cho hàm số \(y=f(x)\) có đồ thị \(y=f'(x)\) cắt trục Ox tại 3 điểm có hoành độ \(a<b<c\) như hình vẽ. Mệnh đề nào dưới đây là đúng ?
- A \(f(a)>f(b)>f(c)\).
- B \(f(c)>f(b)>f(a)\).
- C \(f(c)>f(a)>f(b)\).
- D \(f(b)>f(a)>f(c)\).
Phương pháp giải:
+) \(f'(x)>0\,\,\forall x\in \left( a;b \right)\Rightarrow y=f(x)\) đồng biến trên \(\left( a;b \right)\).
+) \(f'(x)<0\,\,\forall x\in \left( a;b \right)\Rightarrow y=f(x)\) nghịch biến trên \(\left( a;b \right)\).
Lời giải chi tiết:
Quan sát đồ thị của hàm số \(y=f'(x)\), ta thấy:
+) \(f'(x)<0,\,\,\forall x\in \left( a;b \right)\Rightarrow y=f(x)\) nghịch biến trên \(\left( a;b \right)\)\(\Rightarrow f(a)>f(b)\)
+) \(f'(x)>0,\,\,\forall x\in \left( b;c \right)\Rightarrow y=f(x)\) đồng biến trên \(\left( b;c \right)\)\(\Rightarrow f(b)<f(c)\)
Như vậy, \(f(a)>f(b),\,\,f(c)>f(b)\).
Đối chiếu với 4 phương án, ta thấy chỉ có phương án C thỏa mãn.
Chọn: C







