Câu hỏi
Một mạch điện xoay chiều có dạng như hình vẽ trong đó cuộn dây thuần cảm có cảm kháng ZL = 0,5R, tụ điện có dung kháng ZC = 2R. Khi khóa K đặt ở a, thì cường độ dòng điện qua cuộn dây có biểu thức $${i_1} = 0,4\sin \left( {100\pi t + \frac{\pi }{6}} \right)A$$. Hỏi khi khóa K đặt tại b thì dòng điện qua C có biểu thức nào sau đây ?
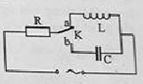
- A \(i = 0,1\sin \left( {100\pi t + \frac{\pi }{2}} \right)A\)
- B \(i = 0,2\sin \left( {100\pi t + \frac{{2\pi }}{3}} \right)A\)
- C \(i = 0,1\sqrt 2 \sin \left( {100\pi t + \frac{\pi }{4}} \right)A\)
- D \(i = 0,2\sin \left( {100\pi t - \frac{\pi }{3}} \right)A\)
Phương pháp giải:
Phương pháp : Áp dụng công thức tính tổng trở và độ lệch pha giữa u,i trong đoạn mạch xoay chiều R,L,C nối tiếp.
Lời giải chi tiết:
Đáp án B
Cách giải:
Khi K ở a thì mạch có R,L \( = > Z = \sqrt {{R^2} + Z_L^2} = \frac{{\sqrt 5 R}}{2} = > {U_0} = {I_0}.Z = 0,2\sqrt 5 R\)
Khi K ở b thì mạch có R,C \(= > Z' = \sqrt {{R^2} + Z_L^2} = \sqrt 5 R = > I{'_0} = \frac{{{U_0}}}{{Z'}} = 0,2A\)
Khi K ở a ta có \(\tan \varphi = \frac{{{Z_L}}}{R} = 0,5 = > \varphi = 26,565 = > {\varphi _u} = 30 + 26,565\)
Khi K ở b ta có \(\tan \varphi = - \frac{{{Z_C}}}{R} = - 2 = > \varphi = 63,435 = > {\varphi _i} = 30 + 26,565 + 63,435 = 120 = \frac{{2\pi }}{3}\)
Vậy khi K ở b thì cường độ dòng điện qua C có biểu thức \(i = 0,2\sin \left( {100\pi t + \frac{{2\pi }}{3}} \right)A\)







