Câu hỏi
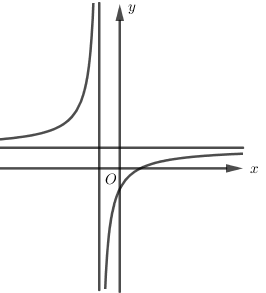
Cho hình vẽ bên là đồ thị hàm số \(y = \frac{{ax + b}}{{cx + d}}\).
Tìm khẳng định đúng trong các khẳng định sau:
- A \(ad > 0,ab < 0\)
- B \(bd > 0,ad > 0\)
- C \(bd > 0,ab > 0\)
- D \(ab < 0,ad < 0\)
Phương pháp giải:
Dựa vào các đường tiệm cận và các giao điểm của đồ thị hàm số với trục tung và trục hoành để chọn được đáp án đúng.
Lời giải chi tiết:
Đồ thị hàm số có đường tiệm cận đứng \(x = - \frac{d}{c} < 0 \Leftrightarrow cd > 0\)
Đồ thị hàm số có đường tiệm cận ngang \(y = \frac{a}{c} > 0 \Rightarrow ac > 0\)
\( \Rightarrow ad{c^2} > 0 \Rightarrow ad > 0 \Rightarrow \) loại đáp án D.
Khi \(x = 0 \Rightarrow y = \frac{b}{d} < 0 \Rightarrow bd < 0 \Rightarrow \) loại B và C.
Chọn A.
Câu hỏi trước
