Câu hỏi
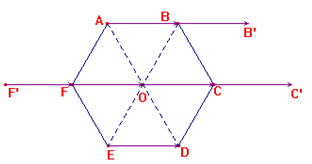
Cho lục giác đều \(ABCDEF\) có tâm \(O\).
a) Số các vecto khác vecto \(\overrightarrow 0 \) và cùng phương với \(\overrightarrow {OA} \) là?
b) Số các vecto bằng vecto \(\overrightarrow {AB} \) là?
c) Hãy vẽ các vecto bằng vecto \(\overrightarrow {AB} \) và có:
+) Các điểm đầu là \(B,\, F, \, C.\)
+) Các điểm cuối là \(F,\, D, \, C.\)
- A a) có 4 vecto; b) có 3 vecto
- B a) có 6 vecto; b) có 2 vecto
- C a) có 8 vecto; b) có 2 vecto
- D a) có 9 vecto; b) có 3 vecto
Lời giải chi tiết:
a) \(\overrightarrow {DA} ,\overrightarrow {AD} ,\overrightarrow {BC} ,\overrightarrow {CB} ,\overrightarrow {AO} ,\overrightarrow {OD} ,\overrightarrow {DO} ,\overrightarrow {FE} ,\overrightarrow {EF} \)
b) \(\overrightarrow {OC} ,\overrightarrow {ED} ,\overrightarrow {FO} \)
c) Trên tia \(AB,\) ta lấy điểm \(B'\) sao cho \(BB' = AB\)
khi đó \(\overrightarrow {BB'} = \overrightarrow {AB} \)
* \(\overrightarrow {FO} \) là vectơ cần tìm
* Trên tia \(OC\) lấy \(C'\) sao cho \(CC' = OC = AB.\)
Do \(CC'//AB \Rightarrow \overrightarrow {CC'} = \overrightarrow {AB} .\)
+) Tương tự.







