Câu hỏi
Cho hàm số \(y=f(x)\) có đồ thị hàm số \(y=f'(x)\) như hình vẽ bên:
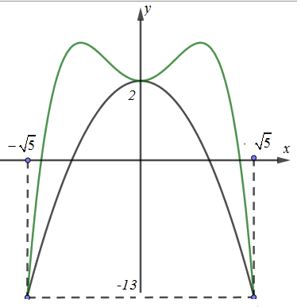
Xét hàm số \(g(x)=2f(x)+2{{x}^{3}}-4x-3m-6\sqrt{5}\) với m là số thực. Để \(g(x)\le 0,\,\,\forall x\in \left[ -\sqrt{5};\sqrt{5} \right]\) thì điều kiện của m là:
- A \(m\ge \frac{2}{3}f\left( \sqrt{5} \right)\).
- B \(m\le \frac{2}{3}f\left( \sqrt{5} \right)\).
- C \(m\ge \frac{2}{3}f\left( -\sqrt{5} \right)-4\sqrt{5}\).
- D \(m\le \frac{2}{3}f\left( 0 \right)-2\sqrt{5}\).
Phương pháp giải:
Tính \(g'\left( x \right)\), giải phương trình \(g'\left( x \right)=0\), xét dấu của \(g'\left( x \right)\).
\(g(x)\le 0,\,\,\forall x\in \left[ -\sqrt{5};\sqrt{5} \right]\Rightarrow \underset{\left[ -\sqrt{5};\sqrt{5} \right]}{\mathop{\max }}\,g\left( x \right)\le 0\)
Lời giải chi tiết:
\(\begin{align} g(x)=2f(x)+2{{x}^{3}}-4x-3m-6\sqrt{5} \\ \Rightarrow g'(x)=2f'(x)+6{{x}^{2}}-4=2\left[ f'(x)+3{{x}^{2}}-2 \right] \\ g'(x)=0\Leftrightarrow f'(x)+3{{x}^{2}}-2=0\Leftrightarrow f'(x)=2-3{{x}^{2}} \\ \end{align}\)
Quan sát đồ thị hàm số \(y=f'(x)\) và \(y=2-3{{x}^{2}}\) ta thấy, 2 đồ thị hàm số trên cắt nhau tại 3 điểm : \((0;2),\,\,(\sqrt{5};-13),\,\,(-\sqrt{5};-13)\) và đồ thị hàm số\(y=f'(x)\) luôn nằm trên đồ thị hàm số \(y=2-3{{x}^{2}}\).
Do đó \(g'(x)\ge 0,\,\,\forall x\in \left[ -\sqrt{5};\sqrt{5} \right],\,\,\,g'(x)=0\Leftrightarrow \left[ \begin{align} x=0 \\ x=\sqrt{5} \\ x=-\sqrt{5} \\ \end{align} \right.\).
Hàm số \(y=g(x)\) đồng biến trên \(\left[ -\sqrt{5};\sqrt{5} \right]\) . Như vậy, để \(g(x)\le 0,\,\,\forall x\in \left[ -\sqrt{5};\sqrt{5} \right]\) thì \(\underset{\left[ -\sqrt{5};\sqrt{5} \right]}{\mathop{Max}}\,g(x)=g(\sqrt{5})\le 0\)
\(\Leftrightarrow 2f(\sqrt{5})+2.{{\left( \sqrt{5} \right)}^{3}}-4.\sqrt{5}-3m-6\sqrt{5}\,\,\le 0\,\,\,\Leftrightarrow 2f(\sqrt{5})-3m\le 0\,\,\,\Leftrightarrow m\ge \frac{2}{3}f\left( \sqrt{5} \right)\) .
Chọn: A







