Câu hỏi
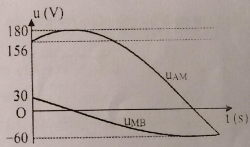
Đặt điện áp xoay chiều AB gồm: đoạn mạch AM chứa điện trở thuần R = 90Ω và tụ điện C = 35,4µF, đoạn mạch MB gồm hộp X chứa 2 trong 3 phần tử mắc nối tiếp (điện trở thuần R0; cuộn cảm thuần có độ tự cảm L0; tụ điện có điện dung C0). Khi đặt vào hai đầu AB một điện thế xoay chiều có tần số 50Hz thì ta được đồ thị sự phụ thuộc của uAM và uMB theo thời gian như hình vẽ (chú ý \(90\sqrt 3 \approx 156\)). Giá trị của các phần tử trong hộp X là
- A R0 = 60Ω; L0 = 165Mh
- B R0 = 30Ω; L0 = 95,5mH
- C R0 = 60Ω; L0 = 61,3mH
- D R0 = 30Ω; L0 = 106mH
Phương pháp giải:
Phương pháp: Sử dụng các công thức của dòng điện xoay chiều kết hợp kĩ năng đọc đồ thị
Lời giải chi tiết:
Đáp án B
Cách giải:
Ta có: R = 90W, ZC = 90W
Từ đồ thị, ta có: ${U_{{0_{AM}}}} = 180V;{U_{{0_{MB}}}} = 60V$
Tại thời điểm t = 0, ta có:
uAM = 156 và đang tăng $ \to {u_{AM}} = 156 = 180c{\text{os}}{\varphi _1} \to {\varphi _1} = - {30^0}$
uMB = 30 và đang giảm $ \to {u_{AM}} = 30 = 60c{\text{os}}{\varphi _2} \to {\varphi _2} = {60^0}$
$ \to {\varphi _2} - {\varphi _1} = {90^0} \to {u_{AM}} \bot {u_{MB}}$
=> hộp X gồm 2 phần tử R0 và L0
${u_{AM}} \bot {u_{MB}} \to \left| {\tan {\varphi _1}\tan {\varphi _2}} \right| = 1 \leftrightarrow \frac{{{Z_{{L_0}}}}}{{{R_0}}}\frac{{{Z_C}}}{R} = 1 \leftrightarrow \frac{{{Z_{{L_0}}}}}{{{R_0}}}\frac{{90}}{{90}} = 1 \to {Z_{{L_0}}} = {R_0}$
Mặt khác, ta có:
$\eqalign{
& {{{U_{{0_{AM}}}}} \over {{U_{{0_{MB}}}}}} = {{{Z_{AM}}} \over {{Z_{MB}}}} = {{180} \over {60}} = 3 \to {Z_{AM}} = 3{Z_{MB}} \leftrightarrow \sqrt {R_0^2 + Z_{{L_0}}^2} = 3.\sqrt {{{90}^2} + {{90}^2}} \cr
& \to {R_0} = {Z_{{L_0}}} = 30\Omega \to \left\{ \matrix{
{R_0} = 30\Omega \hfill \cr
{L_0} = 95,9mH \hfill \cr} \right. \cr} $
=> Chọn B







