Câu hỏi
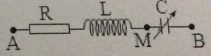
Đặt điện áp xoay chiều u = U0cosωt vào hai đầu đoạn mạch AB như hình vẽ (tụ điện có C thay đổi được). Điều chỉnh C đến giá trị C0 để điện áp hiệu dụng giữa hai đầu tụ điện đạt giá trị cực đại, khi đó điện áp tức thời giữa A và M có giá trị cực đại là 84,5V. Giữ nguyên giá trị C0 của tụ điện. Ở thời điểm t0 điện áp hai đầu tụ điện, cuộn cảm thuần và điện trở có độ lớn lần lượt là 202,8 V, 30 V và uR. Giá trị uR bằng:
- A 50 V
- B 60 V
- C 30 V
- D 40 V
Phương pháp giải:
Phương pháp: Mạch điện xoay chiều có C thay đổi
Lời giải chi tiết:
Đáp án C
Cách giải:
Ta có: \({U_{0RL}} = {u_{AM}}_{\left( {max} \right)} = 84,5V = \sqrt {U_{0R}^2 + U_{0L}^2} \)
uL và uC luôn ngược pha nhau =>$\left| {\frac{{{u_C}}}{{{u_L}}}} \right| = \frac{{{U_{0C}}}}{{{U_{0L}}}} = \frac{{202,8}}{{30}} = 6,76{\text{ }}\left( 1 \right)$
C = C0 thì UCmax : Ta có: $U_{0Cm{\text{ax}}}^2 = U_0^2 + U_{0L}^2 + U_{0R}^2{\text{ }}\left( 2 \right)$
Mặt khác: \(U_0^2 = U_{0R}^2 + {({U_{0L}} - {U_{0Cm{\text{ax}}}}{\text{)}}^2}{\text{ }}\left( 3 \right)\)
Từ (1), (2) và (3) =>
\(2U_0^2 = U_{0Cm{\text{ax}}}^2 - U_{0L}^2 + {({U_{0L}} - {U_{0Cm{\text{ax}}}}{\text{)}}^2} = 6,{76^2}U_{0L}^2 - U_{0L}^2 + 5,{76^2}{U_{0L}}^2 \to U_0^2 = 38,9376{U_{0L}}^2\)
Thay vào (2)
\( \Rightarrow {\text{ }}6,{76^2}{U_{0L}}^2 = {\text{ }}38,9376{U_{0L}}{^2_\;} + {\text{ }}{U_{0RL}}^2 \to {U_{0L}} = \frac{5}{{13}}{U_{0RL}} = 32,5V \to {U_{0R}} = \sqrt {{U_{0RL}}^2 - U_{0L}^2} = 78V\)
Mặt khác, ta có: uL và uR luôn vuông pha nhau:$ \to {\left( {\frac{{{u_L}}}{{{U_{0L}}}}} \right)^2} + {\left( {\frac{{{u_R}}}{{{U_{0R}}}}} \right)^2} = 1 \leftrightarrow {\left( {\frac{{30}}{{32,5}}} \right)^2} + {\left( {\frac{{{u_R}}}{{78}}} \right)^2} = 1 \to {u_R} = 30V$
=> Chọn C







