Phương pháp giải:

Áp dụng phương pháp xác định góc giữa hai mặt phẳng : Góc giữa hai mặt phẳng là góc giữa đường thẳng thuộc hai mặt phẳng cùng vuông góc với giao tuyến của hai mặt phẳng.

Lời giải chi tiết:

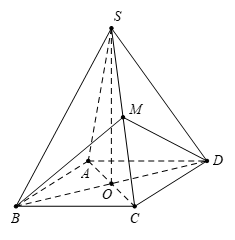
Gọi $M$ là trung điểm của $SC$$\Rightarrow \left\{ \begin{align}BM\bot SC \\ DM\bot SC \\ \end{align} \right.\Rightarrow SC\bot \left( MBD \right).$

Suy ra $\widehat{\left( SBC \right);\left( SCD \right)}=\widehat{\left( MB;MD \right)}=\widehat{BMD}=2\,\,\times \,\,\widehat{\left( SAC \right);\left( SCD \right)}=2\alpha .$

Tam giác $SBC$ đều $\Rightarrow BM=\frac{a\sqrt{6}}{2};$ tam giác $SCD$ đều $\Rightarrow DM=\frac{a\sqrt{6}}{2}.$

Tam giác $MBD$ có $\cos \widehat{BMD}=\frac{B{{M}^{2}}+D{{M}^{2}}-B{{D}^{2}}}{2.BM.DM}=-\,\frac{1}{3}$

$\Rightarrow \,\,2{{\cos }^{2}}\alpha -1=-\frac{1}{3}\Leftrightarrow \cos \alpha =\frac{\sqrt{3}}{3}\,\,\xrightarrow{{}}\,\,\tan \alpha =\sqrt{\frac{1}{{{\cos }^{2}}\alpha }-1}=\sqrt{2}.$

Chọn C