Câu hỏi
Cho hình chóp tam giác đều S. ABC có độ dài cạnh đáy bằng a. Độ dài cạnh bên của hình
chóp bằng bao nhiêu để góc giữa cạnh bên và mặt đáy bằng \({{60}^{0}}\) ?
- A
\(\frac{2a}{\sqrt{3}}\)
- B
\(\frac{a}{6}\)
- C
\(\frac{a\sqrt{3}}{6}\)
- D \(\frac{2a}{3}\)
Phương pháp giải:
Xác định góc giữa đường thẳng và mặt phẳng và sử dụng định lý Pitago trong tam giác vuông
Lời giải chi tiết:
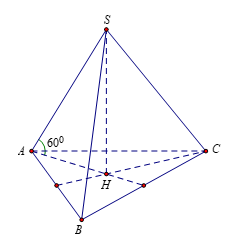
Gọi \(H\) là hình chiếu của \(S\) trên mặt phẳng \(\left( ABC \right)\Rightarrow \) H là tâm tam giác đều \(ABC\)
Tam giác \(ABC\) đều cạnh \(ABC\)\(\Rightarrow \)\(AH=\frac{2}{3}\sqrt{{{a}^{2}}-{{\left( \frac{a}{2} \right)}^{2}}}=\frac{a\sqrt{3}}{3}.\)
Tam giác \(SAH\) vuông tại \(H,\) có \(SA=\frac{AH}{\cos {{60}^{0}}}=\frac{\frac{a\sqrt{3}}{3}}{\frac{1}{2}}=\frac{2a}{\sqrt{3}}.\)
Chọn A.
Câu hỏi trước
