Câu hỏi
Cho \(\Delta ABC,\) đường cao \(AH\) và trung tuyến \(AM.\) Biết \(AH = 12cm;\,\,HB = 9cm;\,\,\,HC = 16cm.\) Tính tỷ số lượng giác của góc \(\angle HAM.\)
- A
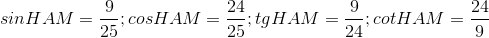
- B
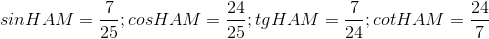
- C
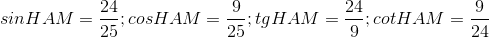
- D
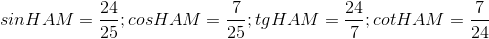
Lời giải chi tiết:
Xét \(\Delta HAB\) và \(\Delta HCA\) ta có:
\(\begin{array}{l} & \frac{{HB}}{{HA}} = \frac{9}{{12}} = \frac{3}{4}\\ & \frac{{HA}}{{HC}} = \frac{{12}}{{16}} = \frac{3}{4}\\ \Rightarrow \frac{{HB}}{{HA}} = \frac{{HA}}{{HC}} = \frac{3}{4}\end{array}\)
Lại có \(\angle AHB = \angle AHC = {90^0}\)\( \Rightarrow HM = HC - MC = 16 - 12,5 = 3,5\,\,cm.\)
\( \Rightarrow \left\{ \begin{array}{l}\angle BAH = \angle HCA\\\angle ABH = \angle HAC\end{array} \right.\) (các góc tương ứng).
Mà \(\angle ABH + \angle BAH = {90^0} \Rightarrow \angle BAH + \angle HAC = {90^0}\)
\( \Rightarrow \Delta ABC\) vuông tại \(A.\)
Theo đề bài ta có \(AM\) là đường trung tuyến của \(\Delta ABC \Rightarrow AM = \frac{1}{2}BC = \frac{1}{2}\left( {HB + HC} \right) = \frac{1}{2}\left( {9 + 16} \right) = 12,5\,\,cm.\)
Xét \(\Delta HAM\) vuông tại \(H\) ta có:
\(\begin{array}{l}\sin \angle HAM = \frac{{HM}}{{AM}} = \frac{{3,5}}{{12,5}} = \frac{7}{{25}} & & & \cos \angle HAM = \frac{{AH}}{{AM}} = \frac{{12}}{{12,5}} = \frac{{24}}{{25}}\\\tan \angle HAM = \frac{{HM}}{{AH}} = \frac{{3,5}}{{12}} = \frac{7}{{24}} &&& \cot \angle HAM = \frac{{AH}}{{HM}} = \frac{{12}}{{3,5}} = \frac{{24}}{7}.\end{array}\)








