 Môn Toán - Lớp 12
Môn Toán - Lớp 12
 40 bài tập trắc nghiệm sự đồng biến nghịch biến của hàm số mức độ vận dụng, vận dụng cao
40 bài tập trắc nghiệm sự đồng biến nghịch biến của hàm số mức độ vận dụng, vận dụng cao
Câu hỏi
Cho hàm số \(y=f\left( x \right)\). Hàm số \(y=f'\left( x \right)\) có đồ thị như hình dưới
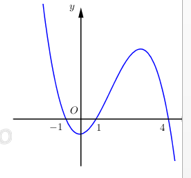
Hàm số \(y=f\left( 3-x \right)\) nghịch biến trên khoảng:
- A
\(\left( 2;4 \right)\)
- B
\(\left( -1;2 \right)\)
- C
\(\left( 2;+\infty \right)\)
- D \(\left( -\infty ;-1 \right)\)
Phương pháp giải:
+) Lập BBT của đồ thị hàm số \(y=f\left( x \right)\) sau đó suy ra đồ thị của hàm số \(y=f\left( -x \right)\) đối xứng với đồ thị hàm số\(y=f\left( x \right)\) qua trục Oy. Và suy ra đồ thị hàm số \(y=f\left( 3-x \right)\) bằng cách tính tiến đồ thị hàm số \(y=f\left( -x \right)\) theo vector \(\left( 3;0 \right)\)
+) Suy ra các khoảng nghịch biến của đồ thị hàm số \(y=f\left( 3-x \right)\).
Lời giải chi tiết:
Dựa vào đồ thị hàm số \(y=f'\left( x \right)\) ta thấy \(f'\left( x \right)=0\Leftrightarrow \left[ \begin{align} x=-1 \\ x=1 \\ x=4 \\ \end{align} \right.\)
\(f'\left( x \right)>0\Leftrightarrow x\in \left( -\infty ;-1 \right)\cup \left( 1;4 \right);\,\,f'\left( x \right)<0\Leftrightarrow x\in \left( -1;1 \right)\cup \left( 4;+\infty \right)\)
Từ đó ta có thể lập được BBT của đồ thị hàm số \(y=f\left( x \right)\) như sau:
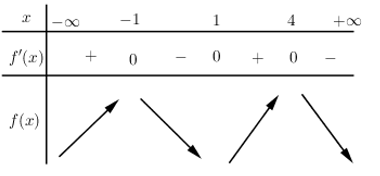
Đồ thị hàm số \(y=f\left( 3-x \right)\) được vẽ bằng cách:
Vẽ đồ thị hàm số \(y=f\left( -x \right)\) đối xứng với đồ thị hàm số \(y=f\left( x \right)\) qua trục Oy, sau đó tịnh tiến đồ thị hàm số \(y=f\left( -x \right)\) theo vector \(\left( 3;0 \right)\)
Đồ thị hàm số \(y=f\left( x \right)\) đồng biến trên \(\left( -\infty ;-1 \right)\) và \(\left( 1;4 \right)\) nên đồ thị hàm số \(y=f\left( -x \right)\) nghịch biến trên \(\left( -4;-1 \right)\) và \(\left( 1;+\infty \right)\).
\(\Rightarrow \) Đồ thị hàm số \(y=f\left( 3-x \right)\) nghịch biến trên \(\left( -1;2 \right)\) và \(\left( 4;+\infty \right)\).
Chọn B.






