Câu hỏi
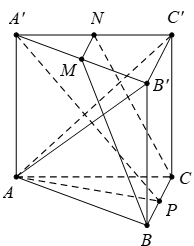
Cho hình lăng trụ tam giác đều \(ABC.{A}'{B}'{C}'\) có \(AB=2\sqrt{3}\) và \(A{A}'=2.\) Gọi \(M,\,\,N,\,\,P\) lần lượt là trung điểm của các cạnh \({A}'{B}',\,\,{A}'{C}'\) và \(BC.\) Côsin của góc tạo bởi hai mặt phẳng \(\left( A{B}'{C}' \right)\) và \(\left( MNP \right)\) bằng
- A \(\frac{6\sqrt{13}}{65}.\)
- B \(\frac{\sqrt{13}}{65}.\)
- C \(\frac{17\sqrt{13}}{65}.\)
- D \(\frac{18\sqrt{63}}{65}.\)
Lời giải chi tiết:
Dễ thấy \(\widehat{\left( A{B}'{C}' \right);\left( MNP \right)}=\widehat{\left( A{B}'{C}' \right);\left( MNCB \right)}\)
\(\begin{align} & ={{180}^{0}}-\widehat{\left( A{B}'{C}' \right);\left( {A}'{B}'{C}' \right)}-\widehat{\left( MNBC \right);\left( {A}'{B}'{C}' \right)} \\ & ={{180}^{0}}-\widehat{\left( {A}'BC \right);\left( ABC \right)}-\widehat{\left( MNBC \right);\left( ABC \right)}. \\\end{align}\)
Ta có \(\widehat{\left( {A}'BC \right);\left( ABC \right)}=\widehat{\left( {A}'P;AP \right)}=\widehat{{A}'PA}=\arctan \frac{2}{3}.\)
Và \(\widehat{\left( MNBC \right);\left( ABC \right)}=\widehat{\left( SP;AP \right)}=\widehat{SPA}=\arctan \frac{4}{3},\) với \(S\) là điểm đối xứng với \(A\) qua \({A}',\) thì \(SA=2\,A{A}'=4.\)
Suy ra \(\cos \widehat{\left( A{B}'{C}' \right);\left( MNP \right)}=\cos \left( {{180}^{0}}-\arctan \frac{2}{3}-\arctan \frac{4}{3} \right)=\frac{\sqrt{13}}{65}.\)
Chọn B.