Phương pháp giải:

+) Lập BBT của đồ thị hàm số \(f\left( x \right)={{x}^{3}}-3x+m\) trên \(\left[ 0;2 \right]\)

+) Xét các trường hợp dấu của các điểm cực trị.

Lời giải chi tiết:

Xét hàm số \(f\left( x \right)={{x}^{3}}-3x+m\) trên \(\left[ 0;2 \right]\) ta có : \(f'\left( x \right)=3{{x}^{2}}-3=0\Leftrightarrow x=\pm 1\)

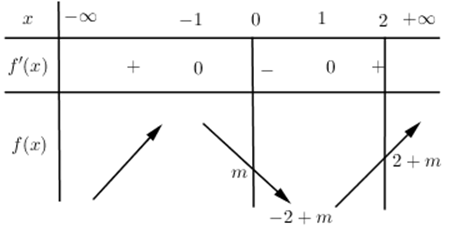
BBT :

TH1 : \(2+m<0\Leftrightarrow m<-2\Rightarrow \underset{\left[ 0;2 \right]}{\mathop{\max }}\,y=-\left( -2+m \right)=2-m\Leftrightarrow 2-m=3\Leftrightarrow m=-1\,\,\left( \,ktm \right)\)

TH2 : \(\left\{ \begin{align}  & m+2>0 \\  & m<0 \\ \end{align} \right.\Leftrightarrow -2<m<0\Leftrightarrow \underset{\left[ 0;2 \right]}{\mathop{\max }}\,y=2-m=3\Leftrightarrow m=-1\,\,\left( tm \right)\)

TH3 :    \(\left\{ \begin{align}  & m>0 \\  & -2+m<0 \\ \end{align} \right.\Leftrightarrow 0<m<2\Leftrightarrow \underset{\left[ 0;2 \right]}{\mathop{\max }}\,y=2+m=3\Leftrightarrow m=1\,\,\left( tm \right)\)

TH4 : \(-2+m>0\Leftrightarrow m>2\Leftrightarrow \underset{\left[ 0;2 \right]}{\mathop{\max }}\,y=2-m=3\Leftrightarrow m=-1\,\,\left( ktm \right)\)

Chọn B.