Câu hỏi
Cho hình trụ có thiết diện qua trục là hình vuông cạnh 2a. Mặt phẳng (P) song song với trục và cách trục một khoảng \(\frac{a}{2}\(. Tính diện tích thiết diện của hình trụ cắt bởi (P).
- A \(2\sqrt{3}{{a}^{2}}\)
- B \({{a}^{2}}\)
- C \(4{{a}^{2}}\)
- D \(\pi {{a}^{2}}\)
Phương pháp giải:
Sử dụng định lý Pytago tính cạnh của thiết diện của hình trụ cắt bới (P).
Lời giải chi tiết:
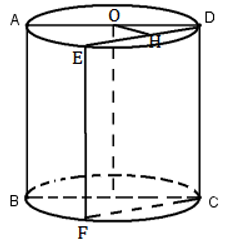
Gọi O là tâm mặt đáy.
Giả sử (P) cắt hình trụ theo thiết diện là CDEF và H là trung điểm của DE ta có \(OH=\frac{a}{2}\)
Xét tam giác vuông ODH có
\(\begin{align} & DH=\sqrt{O{{D}^{2}}-O{{H}^{2}}}=\sqrt{{{a}^{2}}-\frac{{{a}^{2}}}{4}}=\frac{a\sqrt{3}}{2}\Rightarrow DE=a\sqrt{3} \\ & CD=2a \\ & \Rightarrow {{S}_{CDEF}}=DE.CD=a\sqrt{3}.2a=2\sqrt{3}{{a}^{2}} \\ \end{align}\)
Chọn A.
Câu hỏi trước
