Câu hỏi
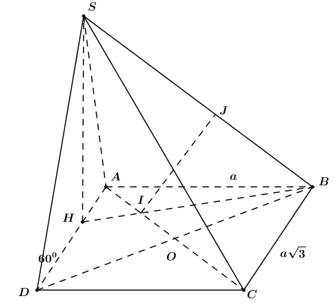
Cho hình chóp SABCD có đáy ABCD là hình chữ nhật tâm O, \(AB=a;\ BC=a\sqrt{3}.\) Tam giác SAO cân tại S, mặt phẳng (SAD) vuông góc với mặt phẳng (ABCD), góc giữa SD và (ABCD) bằng \({{60}^{0}}.\) Khoảng cách giữa hai đường thẳng SB và AC:
- A \(\frac{a\sqrt{3}}{2}\)
- B \(\frac{3a}{2}\)
- C \(\frac{a}{2}\)
- D \(\frac{3a}{4}\)
Phương pháp giải:
+) Vận dụng cách tìm góc giữa hai mặt phẳng và cách tìm khoảng cách giữa đường thẳng và mặt phẳng.
Lời giải chi tiết:
Gọi I là trung điểm của \(AO,\ \left( \alpha \right)\) là mặt phẳng trung trực của đoạn \(AO\).
Gọi \(H=\left( \alpha \right)\cap AD.\)
Từ H dựng đường thẳng \(d\bot \left( ABCD \right).\)
Lấy \(S\in d,\) như thế ta có hình chóp thỏa mãn bài toán.
Ta có góc giữa đường thẳng SD với (ABCD) là góc \(\widehat{SDA}={{60}^{0}}.\)
\(\Rightarrow \tan \widehat{SAD}=\frac{SH}{HD}.\)
Áp dụng định lý Pi-ta-go ta có: \(AC=\sqrt{A{{B}^{2}}+B{{C}^{2}}}=2a.\)
Ta có: \(\Delta AIH\backsim \Delta ADC\ \left( g-g \right)\Rightarrow \frac{AI}{AD}=\frac{AH}{AC}\Rightarrow AH=\frac{AI.AC}{AD}=\frac{A{{C}^{2}}}{4AD}=\frac{a\sqrt{3}}{3}.\) \(\begin{align} & \Rightarrow DH=AD-AH=a\sqrt{3}-\frac{a\sqrt{3}}{3}=\frac{2a\sqrt{3}}{3}. \\ & \Rightarrow SH=DH.\tan {{60}^{0}}=\frac{2a\sqrt{3}}{3}.\sqrt{3}=2a. \\ \end{align}\)
Ta có \(AO=BO=AB=a\Rightarrow \Delta AOB\) là tam giác đều.
\(\Rightarrow IB\bot AO\Rightarrow B\in \left( SHI \right)\Rightarrow H,\ I,\ B\) thẳng hàng.
Ta có: \(\left\{ \begin{align} & AC\bot SH \\ & AC\bot BH \\ \end{align} \right.\Rightarrow AC\bot \left( SHB \right)\Rightarrow AC\bot SB.\)
Gọi J là hình chiếu của I lên SB, khi đó ta được \(IJ=d\left( AC,\ SB \right).\)
Ta có:
\(\begin{align} & HB=\sqrt{A{{B}^{2}}+A{{H}^{2}}}=\frac{2a\sqrt{3}}{3}. \\ & \tan \widehat{SHB}=\frac{SH}{HB}=\sqrt{3}\Rightarrow \widehat{SBH}={{60}^{0}}. \\ & \Rightarrow IJ=BI.\sin {{60}^{0}}=\frac{3a}{4}. \\ \end{align}\)
Chọn D.