Câu hỏi
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thang vuông tại \(A\) và \(D\), đáy lớn \(AB\); cạnh bên \(SA\) vuông góc với đáy. Gọi \(Q\) là điểm trên cạnh \(SA\) và \(Q\ne A,\) \(Q\ne S\); \(M\) là điểm trên đoạn \(AD\) và \(M\ne A\). Mặt phẳng \(\left( \alpha \right)\) qua \(QM\) và vuông góc với mặt phẳng \(\left( SAD \right)\). Thiết diện tạo bởi \(\left( \alpha \right)\) với hình chóp đã cho là:
- A
tam giác.
- B
hình thang cân.
- C
hình thang vuông.
- D hình bình hành.
Phương pháp giải:
Sử dụng các định lí về hai mặt phẳng vuông góc
Lời giải chi tiết:
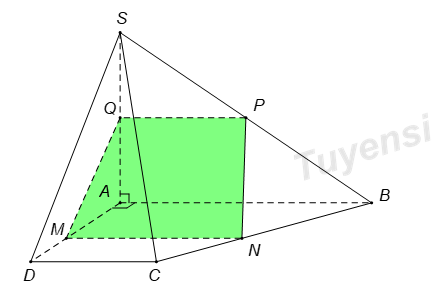
Ta có \(\left\{ \begin{array}{l}AB \bot AD\\AB \bot SA\end{array} \right. \Rightarrow AB \bot \left( {SAD} \right)\). Mà \(\left( \alpha \right)\bot \left( SAD \right)\) suy ra \(AB\parallel \left( \alpha \right)\).
Qua \(M\) kẻ đường thẳng song song với \(AB\) cắt \(BC\) tại \(N\).
Qua \(E\) kẻ đường thẳng song song với \(AB\) cắt \(SB\) tại \(P\).
Khi đó thiết diện là hình thang \(MNPQ\) (do \(MN\parallel PQ\().
Vì \(AB\bot \left( SAD \right)\) suy ra \(MN\bot \left( SAD \right)\) nên \(MN\bot MQ\).
Do đó thiết diện \(MNPQ\) là hình thang vuông tại Q và \(M\).
Chọn C







