Phương pháp giải:

Tìm các giá trị cực đại và cực tiểu của hàm số:

- Bước 1: Tìm tập xác định của hàm số.

- Bước 2: Tính \(f'\left( x \right)\), tìm các điểm tại đó \(f'\left( x \right)=0\) hoặc không xác định.

- Bước 3: Lập bảng biến thiên và kết luận.

+ Tại các điểm mà đạo hàm đổi dấu từ âm sang dương thì đó là điểm cực tiểu của hàm số.

+ Tại các điểm mà đạo hàm đổi dấu từ dương sang âm thì đó là điểm cực đại của hàm số.

Lời giải chi tiết:

TXĐ: \(D=R\).

Ta có: \(y={{x}^{3}}-3{{x}^{2}}+1\Rightarrow y'=3{{x}^{2}}-6x=0\Leftrightarrow 3x\left( x-2 \right)=0\Leftrightarrow \left[ \begin{align}  & x=0 \\  & x=2 \\ \end{align} \right.\)

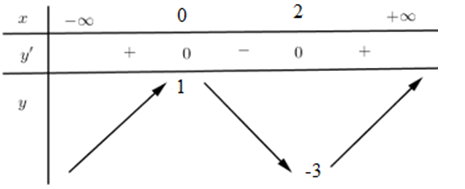
Bảng biến thiên:

Quan sát bảng biến thiên ta thấy giá trị cực đại \({{y}_{CD}}=1\) và giá trị cực tiểu \({{y}_{CT}}=-3\).

Vậy tích \({{y}_{CD}}.{{y}_{CT}}=-3\).

Chọn B.