Phương pháp giải:

Áp dụng phương pháp tìm góc giữa đường thẳng và mặt phẳng – hệ thức lượng trong tam giác vuông để giải quyết yêu cầu của bài toán

Lời giải chi tiết:

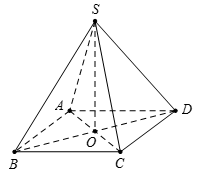
Gọi O là tâm mặt đáy (ABCD), suy ra \(SO \bot \left( {ABCD} \right)\).

Vì \(SO \bot \left( {ABCD} \right)\)\( \Rightarrow \)OA là hình chiếu của SA trên mp(ABCD).

Do đó \(\widehat {\left( {SA;\left( {ABCD} \right)} \right)} = \widehat {\left( {SA;AO} \right)} = \widehat {SAO}.\)

Tam giác vuông SAO, có

\(\tan \widehat {SAO} = \frac{{SO}}{{AO}} = \frac{{\sqrt {S{B^2} - B{O^2}} }}{{AO}} = \frac{{\sqrt {S{B^2} - {{\left( {\frac{{BD}}{2}} \right)}^2}} }}{{\frac{{AC}}{2}}} = \frac{{\sqrt {{3^2} - {{\left( {\frac{{2\sqrt 2 }}{2}} \right)}^2}} }}{{\frac{{2\sqrt 2 }}{2}}} = \frac{{\sqrt {14} }}{2}.\)

Chọn D.