Phương pháp giải:

Sử dụng các công thức tính diện tích xung quanh, diện tích toàn phần và thể tích của hình trụ.

Lời giải chi tiết:

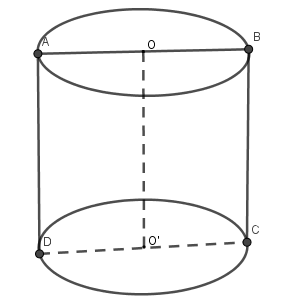
Thiết diện qua trục là hình vuông ABCD có diện tích là 9 nên \(A{{B}^{2}}=9\Rightarrow AB=3=BC=O{O}';OA=\frac{3}{2}\).

Vậy khối trụ có đường sinh là 3, bán kính \(\frac{3}{2}\).

Thể tích khối trụ: \(V=\pi .O{{A}^{2}}.O{O}'=\pi .\frac{9}{4}.9=\frac{81\pi }{4}\).

Diện tích xuang quanh \({{S}_{xq}}=2\pi OA.BC=2.\pi .\frac{3}{2}.3=9\pi \).

Diện tích toàn phần \({{S}_{tp}}=2\pi OA.BC+2\pi .O{{A}^{2}}=2.\pi .\frac{3}{2}.3+2\pi .\frac{9}{4}=\frac{27\pi }{2}\).

Chọn A.