Phương pháp giải:

+) Nhớ lại lăng trụ tam giác đều là lăng trụ đứng có đáy là tam giác đều.

+) Tìm góc giữa hai mặt phẳng  (P) và (Q) như sau:

-Xác định giao tuyến d của (P) và (Q)

-Trong (P) xác định d’ vuông góc với d, trong (Q) xác định d’’ vuông góc với d sao cho d’ cắt d’’.

-Góc giữa (P) và (Q) là góc giữa d’ và d’’.

+) Xác định chiều cao của hình chóp A.BCC’B’.

+) Sử dụng công thức tính thể tích khối chóp: \(V=\frac{1}{3}h.S\) với \(h\) là chiều cao hình chóp và \(S\) là diện tích đáy.

Lời giải chi tiết:

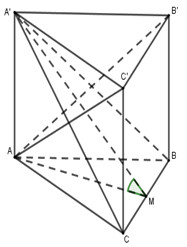
Lấy M là trung điểm của BC. Vì tam giác ABC đều nên \(AM\bot BC\).

Vì ABC.A’B’C’ là lăng trụ đều nên A’C=A’B. Trong tam giác cân A’BC thì \({A}'M\bot BC\).

Từ đó ta có: \(\left\{ \begin{array}{l}BC \bot A'M \subset \left( {A'BC} \right)\\BC \bot AM \subset \left( {ABC} \right)\\A'M \cap AM = \left\{ M \right\}\end{array} \right.\)suy ra góc giữa (A’BC) và (ABC) là góc giữa AM và A’M\(\Rightarrow \widehat{{A}'MA}=60{}^\circ \).

Xét tam giác ABC đều cạnh a có AM là trung tuyến cũng là đường cao, theo Pytago ta  tính được \(AM=\sqrt{A{{B}^{2}}-B{{M}^{2}}}=\dfrac{a\sqrt{3}}{2}\).

Xét tam giác A’AM vuông tại A, có \(A{A}'=AM.\tan \,\widehat{{A}'MA}=AM.\tan 60{}^\circ =\dfrac{a\sqrt{3}}{2}.\sqrt{3}=\dfrac{3a}{2}\).

\(\Rightarrow C{C}'=A{A}'=\dfrac{3a}{2},BC=a,AM=\dfrac{a\sqrt{3}}{2}\).

Lại có \(\left\{ \begin{array}{l}AM \bot BC\\AM \bot CC'\,\left( {{\rm{do}}\,\,CC' \bot\left( {ABC} \right)} \right)\end{array} \right. \Rightarrow AM \bot \left( {BCC'B'} \right)\).

\(\Rightarrow {{V}_{A.BC{C}'{B}'}}=\dfrac{1}{3}AM.{{S}_{BC{C}'{B}'}}\). Mà \(BC{C}'{B}'\) là hình chữ nhật nên \({{S}_{BC{C}'{B}'}}=BC.C{C}'=a.\dfrac{3a}{2}=\dfrac{3{{a}^{2}}}{2}\).

\(\Rightarrow {{V}_{A.BC{C}'{B}'}}=\dfrac{1}{3}.\dfrac{a\sqrt{3}}{2}.\dfrac{3{{a}^{2}}}{2}=\dfrac{{{a}^{3}}\sqrt{3}}{4}\).

Chọn A.