Câu hỏi
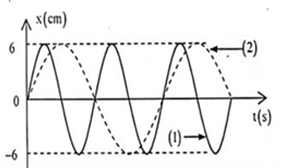
Đồ thị li độ theo thời gian của chất điểm 1 (đường 1) và chất điểm 2 (đường 2) như hình vẽ, tốc độ cực đại của chất điểm 2 là \(3\pi \,\,cm/s\). Không kể thời điểm t = 0, thời điểm hai chất điểm có cùng li độ lần thứ 5 là
- A 5,25 s.
- B 4,33 s.
- C 4,67 s.
- D 5,0 s.
Phương pháp giải:
Sử dụng mối liên hệ giữa vòng tròn lượng giác và dao động điều hòa.
Lời giải chi tiết:
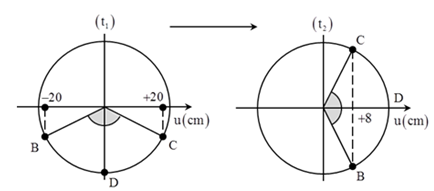
+ Dựa vào hình vẽ ta có:\(\sin {{\Delta \varphi } \over 2} = {{20} \over A}\) và \(\cos {{\Delta \varphi } \over 2} = {8 \over A}.\)
+ Mặc khác \({\sin ^2}\left( {{{\Delta \varphi } \over 2}} \right) + {\cos ^2}\left( {{{\Delta \varphi } \over 2}} \right) = 1 \Rightarrow A = \sqrt {{{20}^2} + {8^2}} = 4\sqrt {29} \,\,mm.\)
+ Tại thời điểm điểm D đang ở biên dương, thời điểm ứng với góc quét \(\alpha = \omega t = {{2\pi } \over 5}\,\,rad.\)
+ Vậy li độ của điểm D khi đó sẽ là: \({u_D} = A\sin \left( \alpha \right) = 6,6\,\,mm.\)
Tốc độ dao động của D:
\(v = \omega \sqrt {{A^2} - u_D^2} = 64,41\,\,{{mm}/s}.\)
Chọn A.